题目内容
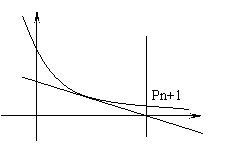 点
点![]() 在曲线
在曲线![]() 上,曲线C在
上,曲线C在![]() 处的切线
处的切线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,直线
,直线![]() :
:![]() 与曲线C相交于点
与曲线C相交于点![]() ,(
,(![]() ).由曲线
).由曲线![]() 和直线
和直线![]() ,
,![]() 围成的图形面积记为
围成的图形面积记为![]() ,已知
,已知![]() .
.
(1)证明:![]() ;
;
(2)求![]() 关于
关于![]() 的表达式;
的表达式;
(3)若数列![]() 的前
的前![]() 项之和为
项之和为![]() ,
,
求证:![]() (
(![]() ).
).
(Ⅰ)证明:因为![]() ,所以
,所以![]() ,则切线
,则切线![]() 的斜率
的斜率![]() ,所以切线
,所以切线![]() 的方程
的方程
为![]() ,令
,令![]() ,得
,得![]() ,即
,即![]() ……………………2分
……………………2分
(Ⅱ)解:因为![]() ,所以
,所以![]() ,
,
所以![]() ………………5分
………………5分
(Ⅲ)证明:因为![]() ,
,
所以![]() ,又
,又![]() ,
,
故要证![]() ,只要证
,只要证![]() ,即要证
,即要证![]() ………………………7分
………………………7分
下用数学归纳法(或用二项式定理,或利用函数的单调性)等方法来
证明![]() (略)………………………………………………………………10分
(略)………………………………………………………………10分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 点
点