题目内容
点 在曲线 上,曲线C在点 处的切线 与 轴相交于点 ,直线 : 与曲线C相交于点 ,( ).由曲线 和直线 , 围成的图形面积记为 ,已知 .
(Ⅰ)证明: ;
(Ⅱ)求 关于 的表达式;
(Ⅲ)记数列 的前 项之和为 ,
求证: ( ).
【答案】
(Ⅰ)证明:因为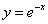 ,所以
,所以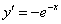 ,则切线
,则切线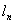 的斜率
的斜率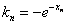 ,所以切线
,所以切线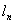 的方程
的方程
为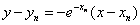 ,令
,令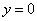 ,得
,得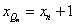 ,即
,即 ……………………2分
……………………2分
(Ⅱ)解:因为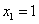 ,所以
,所以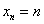 ,
,
所以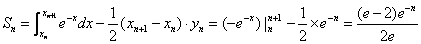 ………………5分
………………5分
(Ⅲ)证明:因为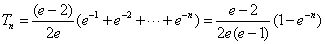 ,
,
所以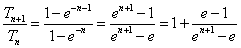 ,又
,又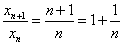 ,
,
故要证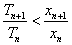 ,只要证
,只要证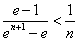 ,即要证
,即要证 ………………………7分
………………………7分
下用数学归纳法(或用二项式定理,或利用函数的单调性)等方法来
证明 (略)…………………………………………………………………10分
(略)…………………………………………………………………10分

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
 在曲线
在曲线 上,
上, 为曲线在点
为曲线在点 B.
B. C.
C. D.
D.
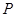 在曲线
在曲线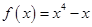 上,曲线在点
上,曲线在点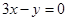 ,则点
,则点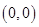 B.
B.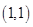 C.
C.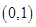 D.
D.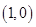
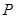 在曲线
在曲线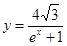 上,
上,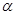 为曲线在点
为曲线在点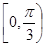 B.
B.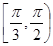 C.
C.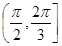 D.
D.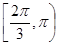
 ,点
,点 在曲线
在曲线 上,曲线
上,曲线 ,点
,点 、
、 为曲线
为曲线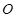 为坐标原点。
为坐标原点。 为曲线
为曲线 最大值;
最大值; 为直径的圆过点
为直径的圆过点 ,求证:直线
,求证:直线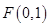 ,直线
,直线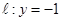 ,过点
,过点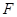 且与直线
且与直线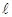 相切的动圆圆心
相切的动圆圆心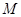 的
的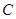 .
.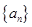 的前
的前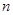 项和为
项和为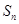 ,且满足:点
,且满足:点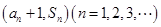
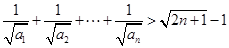 .
.