题目内容
已知点P在曲线![]() 上,曲线C在点P处的切线与函数y=kx(k>0)的图象交于点A,与x轴交于点B,设点P的横坐标为t,点A,B的横坐标分别为xA,xB,记f(t)=xA·xB
上,曲线C在点P处的切线与函数y=kx(k>0)的图象交于点A,与x轴交于点B,设点P的横坐标为t,点A,B的横坐标分别为xA,xB,记f(t)=xA·xB
Ⅰ)求f(t)的解析式
Ⅱ)设数列{an}(n≥1,n∈N)满足a1=1,an=f(![]() )(n≥2),求数列{an}的通项公式
)(n≥2),求数列{an}的通项公式
Ⅲ)在Ⅱ)的条件下,当1<k<3时,证明不等式![]()
答案:
解析:
解析:
|
(1)解: 切线方程为 与 令y=0得: (2)由 两边取倒数得: 或是各项为0的常数列(k=3时),此时 当k=3时也符合上式 (3)作差得: 其中 由于 原式得证 14分. |

练习册系列答案
相关题目
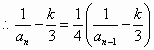 7分
7分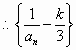 是以
是以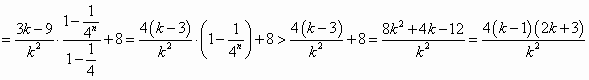 当
当 如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,
如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形, 如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,
如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形, ,|AN|=3,且|BN|=6.
,|AN|=3,且|BN|=6.