题目内容
已知函数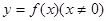 对于任意的
对于任意的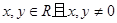 满足
满足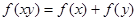 .
.
(1)求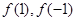 的值;
的值;
(2)求证: 为偶函数;
为偶函数;
(3)若 在
在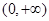 上是增函数,解不等式
上是增函数,解不等式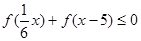
(1)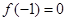 。
。
(2)令 ,得
,得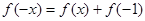 ,可得
,可得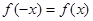 。
。
(3)不等式的解集为:[-1,0)∪(0,2]∪[3,5)∪(5,6]。
解析试题分析:(1)解:∵对于任意的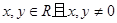 满足
满足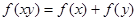
∴令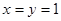 ,得到:
,得到: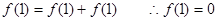
令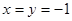 ,得到:
,得到: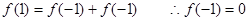 4分
4分
(2)证明:有题可知,令 ,得
,得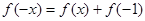
∵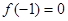 ∴
∴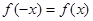 ∴
∴ 为偶函数; 8分
为偶函数; 8分
(3)由(2) 函数 是定义在非零实数集上的偶函数.
是定义在非零实数集上的偶函数.
∴不等式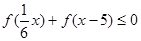 可化为
可化为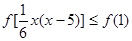
∴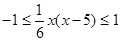 .即:
.即: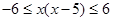 且
且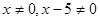
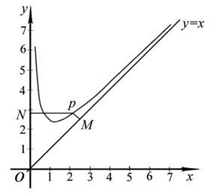
在坐标系内,如图函数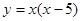 图象与
图象与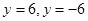 两直线.
两直线.
由图可得x∈[-1,0)∪(0,2]∪[3,5)∪(5,6]
故不等式的解集为:[-1,0)∪(0,2]∪[3,5)∪(5,6] 12分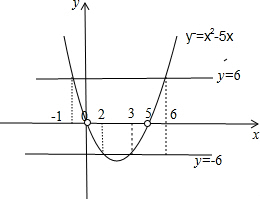
考点:抽象函数,函数的奇偶性,函数的图象,抽象不等式。
点评:中档题,抽象函数问题,往往利用“赋值法”。抽象不等式问题,往往要利用函数的单调性,结合函数的图象分析得解。

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 、圆心角为
、圆心角为 的扇形的弧上任取一点
的扇形的弧上任取一点 ,作扇形的内接矩形
,作扇形的内接矩形 ,使点
,使点 在
在 上,点
上,点 在
在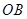 上,设矩形
上,设矩形 ,
,
 ,将
,将 的函数关系式;
的函数关系式; ,将
,将 的函数关系式;
的函数关系式;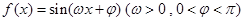 在一个周期内的部分对应值如下表:
在一个周期内的部分对应值如下表:
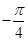

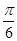

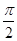
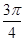


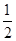
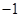
 的解析式;
的解析式;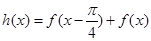 ,
,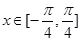 ,求
,求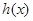 的最大值和最小值.
的最大值和最小值. 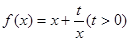 和点
和点 ,过点
,过点 作曲线
作曲线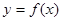 的两条切线
的两条切线 、
、 ,切点分别为
,切点分别为 、
、 .
.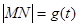 ,试求函数
,试求函数 的表达式;
的表达式; ,使得
,使得 三点共线.若存在,求出
三点共线.若存在,求出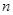 ,在区间
,在区间 内总存在
内总存在 个实数
个实数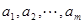 ,
, ,使得不等式
,使得不等式 成立,求
成立,求 的最大值.
的最大值.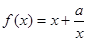 定义域为
定义域为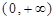 ,且
,且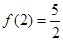 .设点
.设点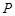 是函数图像上的任意一点,过点
是函数图像上的任意一点,过点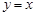 和
和  轴的垂线,垂足分别为
轴的垂线,垂足分别为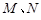 .
.
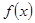 的单调递减区间(不必证明);
的单调递减区间(不必证明);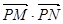 是否为定值?若是,则求出该定值,若不是,则说明理由;
是否为定值?若是,则求出该定值,若不是,则说明理由;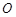 为坐标原点,求四边形
为坐标原点,求四边形 面积的最小值.
面积的最小值. 人,(
人,( ,且
,且 为偶数),每人每年可创利
为偶数),每人每年可创利 万元。据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年可多创利
万元。据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年可多创利 万元,但公司需支付下岗职员每人每年
万元,但公司需支付下岗职员每人每年 万元的生活费,并且该公司正常运转所需人数不得小于现有员工的
万元的生活费,并且该公司正常运转所需人数不得小于现有员工的 ,为获得最大的经济效益,该公司应裁员多少人?
,为获得最大的经济效益,该公司应裁员多少人? (万元)随投资收益
(万元)随投资收益 (万元)的增加而增加,但奖金总数不超过9万元,同时奖金不超过投资收益的20%.
(万元)的增加而增加,但奖金总数不超过9万元,同时奖金不超过投资收益的20%. 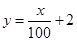 ;②
;②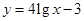 .
. 与
与 ,如果对任意
,如果对任意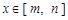 ,均有
,均有 与
与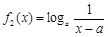 (a > 0且
(a > 0且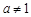 ),给定区间
),给定区间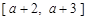 .
.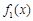 与
与 在给定区间
在给定区间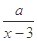 +10(x-6)2,(其中3<x<6,
+10(x-6)2,(其中3<x<6, 为常数,)已知销售价格为5元/千克时,每日可售出该商品11千克。
为常数,)已知销售价格为5元/千克时,每日可售出该商品11千克。