题目内容
已知向量 ,
, ,设函数
,设函数 ,
, .
.
(1)求 的最小正周期与最大值;
的最小正周期与最大值;
(2)在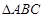 中,
中, 分别是角
分别是角 的对边,若
的对边,若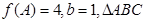 的面积为
的面积为 ,求
,求 的值.
的值.
【答案】
(Ⅰ)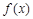 的最小正周期为
的最小正周期为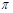 ,最大值为5;(Ⅱ)
,最大值为5;(Ⅱ)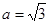
【解析】
试题分析:(Ⅰ)先由向量的数量积坐标运算,得到函数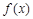
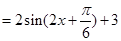 ,从而确定函数的最小正周期和最大值;(Ⅱ)先由已知条件及(Ⅰ)中所求的解析式可得
,从而确定函数的最小正周期和最大值;(Ⅱ)先由已知条件及(Ⅰ)中所求的解析式可得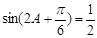 ,解得
,解得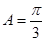 ,再由面积为
,再由面积为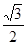 得
得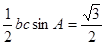 从而解得
从而解得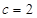 ,由余弦定理得
,由余弦定理得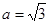 .此题主要是考查三角恒等变换和解三解形.
.此题主要是考查三角恒等变换和解三解形.
试题解析:(1)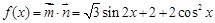 2分
2分
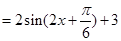 4分
4分
∴ 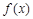 的最小正周期为
的最小正周期为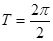 =
=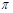 ,
5分
,
5分
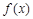 的最大值为5.
6分
的最大值为5.
6分
(2)由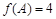 得,
得,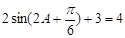 ,即
,即 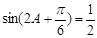 ,
,
∵ 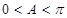 , ∴
, ∴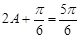 ,
,
∴ 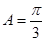 8分
8分
又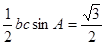 , 即
, 即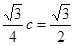 ,
,
∴ 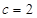 10分
10分
由余弦定理得,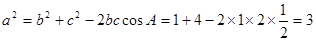 ∴
∴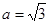
考点:1.三角恒等变换;2.余弦定理的应用

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
 ,
, ,设函数
,设函数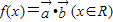 的图象关于直线
的图象关于直线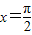 对称,其中ω为常数,且ω∈(0,1).
对称,其中ω为常数,且ω∈(0,1). ,再将所得图象向右平移
,再将所得图象向右平移 个单位,纵坐标不变,得到y=h(x)的图象,若关于x的方程h(x)+k=0在区间
个单位,纵坐标不变,得到y=h(x)的图象,若关于x的方程h(x)+k=0在区间 上有且只有一个实数解,求实数k的取值范围.
上有且只有一个实数解,求实数k的取值范围. ,
, ,设函数
,设函数 •
• ,若函数g(x)的图象与f(x)的图象关于坐标原点对称.
,若函数g(x)的图象与f(x)的图象关于坐标原点对称. ]上的最大值,并求出此时x的值;
]上的最大值,并求出此时x的值; ,b+c=7,△ABC的面积为2
,b+c=7,△ABC的面积为2 ,求边a的长.
,求边a的长. ,
, ,设函数
,设函数 ,x∈R.
,x∈R. ,求函数f(x)值域.
,求函数f(x)值域. ,
, ,设函数
,设函数 ,x∈R.
,x∈R. ,求函数f(x)值域.
,求函数f(x)值域. ,
, ,设函数
,设函数 .
. 的最小正周期;
的最小正周期; 中,若
中,若 的面积为
的面积为 ,求实数
,求实数 的值.
的值.