题目内容
已知向量 ,
, ,设函数
,设函数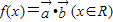 的图象关于直线
的图象关于直线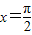 对称,其中ω为常数,且ω∈(0,1).
对称,其中ω为常数,且ω∈(0,1).(Ⅰ)求函数f(x)的表达式;
(Ⅱ)若将y=f(x)图象上各点的横坐标变为原来的
 ,再将所得图象向右平移
,再将所得图象向右平移 个单位,纵坐标不变,得到y=h(x)的图象,若关于x的方程h(x)+k=0在区间
个单位,纵坐标不变,得到y=h(x)的图象,若关于x的方程h(x)+k=0在区间 上有且只有一个实数解,求实数k的取值范围.
上有且只有一个实数解,求实数k的取值范围.
【答案】分析:(Ⅰ)利用向量的数量积公式化简函数,结合函数的图象关于直线 对称,且ω∈(0,1),即可求得函数f(x)的表达式;
对称,且ω∈(0,1),即可求得函数f(x)的表达式;
(Ⅱ)确定h(x)=2sin(2x- ),关于x的方程h(x)+k=0在区间
),关于x的方程h(x)+k=0在区间 上有且只有一个实数解,等价于2sint+k=0在
上有且只有一个实数解,等价于2sint+k=0在 上有且只有一个实数解,由此可得结论.
上有且只有一个实数解,由此可得结论.
解答:解:(Ⅰ)∵向量 ,
, ,
,
∴ =(cos2ωx-sin2ωx,sinωx)•
=(cos2ωx-sin2ωx,sinωx)• =
= cos2ωx+sin2ωx=2sin(2ωx+
cos2ωx+sin2ωx=2sin(2ωx+ )
)
∵函数图象关于直线 对称,∴2sin(πω+
对称,∴2sin(πω+ )=±2
)=±2
∴πω+ =kπ+
=kπ+ (k∈Z),即ω=k+
(k∈Z),即ω=k+ (k∈Z)
(k∈Z)
∵ω∈(0,1),∴k=0,ω=
∴f(x)=2sin( x+
x+ );
);
(Ⅱ)若将y=f(x)图象上各点的横坐标变为原来的 ,再将所得图象向右平移
,再将所得图象向右平移 个单位,纵坐标不变,得到y=h(x)=2sin(2x-
个单位,纵坐标不变,得到y=h(x)=2sin(2x- )的图象,
)的图象,
令2x- =t,∵x∈
=t,∵x∈ ,∴
,∴
∴关于x的方程h(x)+k=0在区间 上有且只有一个实数解,即2sint+k=0在
上有且只有一个实数解,即2sint+k=0在 上有且只有一个实数解,
上有且只有一个实数解,
即y=2sint, 的图象与y=-k有且只有一个交点,
的图象与y=-k有且只有一个交点,
∴- <k≤
<k≤ 或k=-2.
或k=-2.
点评:本题考查向量的数量积运算,考查函数解析式的确定,考查图象的变换,考查解的问题,确定函数的解析式是关键.
 对称,且ω∈(0,1),即可求得函数f(x)的表达式;
对称,且ω∈(0,1),即可求得函数f(x)的表达式;(Ⅱ)确定h(x)=2sin(2x-
 ),关于x的方程h(x)+k=0在区间
),关于x的方程h(x)+k=0在区间 上有且只有一个实数解,等价于2sint+k=0在
上有且只有一个实数解,等价于2sint+k=0在 上有且只有一个实数解,由此可得结论.
上有且只有一个实数解,由此可得结论.解答:解:(Ⅰ)∵向量
 ,
, ,
,∴
 =(cos2ωx-sin2ωx,sinωx)•
=(cos2ωx-sin2ωx,sinωx)• =
= cos2ωx+sin2ωx=2sin(2ωx+
cos2ωx+sin2ωx=2sin(2ωx+ )
)∵函数图象关于直线
 对称,∴2sin(πω+
对称,∴2sin(πω+ )=±2
)=±2∴πω+
 =kπ+
=kπ+ (k∈Z),即ω=k+
(k∈Z),即ω=k+ (k∈Z)
(k∈Z)∵ω∈(0,1),∴k=0,ω=

∴f(x)=2sin(
 x+
x+ );
);(Ⅱ)若将y=f(x)图象上各点的横坐标变为原来的
 ,再将所得图象向右平移
,再将所得图象向右平移 个单位,纵坐标不变,得到y=h(x)=2sin(2x-
个单位,纵坐标不变,得到y=h(x)=2sin(2x- )的图象,
)的图象,令2x-
 =t,∵x∈
=t,∵x∈ ,∴
,∴
∴关于x的方程h(x)+k=0在区间
 上有且只有一个实数解,即2sint+k=0在
上有且只有一个实数解,即2sint+k=0在 上有且只有一个实数解,
上有且只有一个实数解,即y=2sint,
 的图象与y=-k有且只有一个交点,
的图象与y=-k有且只有一个交点,∴-
 <k≤
<k≤ 或k=-2.
或k=-2.点评:本题考查向量的数量积运算,考查函数解析式的确定,考查图象的变换,考查解的问题,确定函数的解析式是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
, ,设函数
,设函数 的图象关于直线
的图象关于直线 对称,其中ω为常数,且ω∈(0,1).
对称,其中ω为常数,且ω∈(0,1). ,再将所得图象向右平移
,再将所得图象向右平移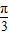 个单位,纵坐标不变,得到y=h(x)的图象,若关于x的方程h(x)+k=0在区间
个单位,纵坐标不变,得到y=h(x)的图象,若关于x的方程h(x)+k=0在区间 上有且只有一个实数解,求实数k的取值范围.
上有且只有一个实数解,求实数k的取值范围. ,
, ,设函数
,设函数 的图象关于直线
的图象关于直线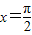 对称,其中ω为常数,且ω∈(0,1).
对称,其中ω为常数,且ω∈(0,1). ,再将所得图象向右平移
,再将所得图象向右平移 个单位,纵坐标不变,得到y=h(x)的图象,若关于x的方程h(x)+k=0在区间
个单位,纵坐标不变,得到y=h(x)的图象,若关于x的方程h(x)+k=0在区间 上有且只有一个实数解,求实数k的取值范围.
上有且只有一个实数解,求实数k的取值范围. ,
, ,设函数
,设函数 的图象关于直线
的图象关于直线 对称,其中ω为常数,且ω∈(0,1).
对称,其中ω为常数,且ω∈(0,1). ,再将所得图象向右平移
,再将所得图象向右平移 个单位,纵坐标不变,得到y=h(x)的图象,若关于x的方程h(x)+k=0在区间
个单位,纵坐标不变,得到y=h(x)的图象,若关于x的方程h(x)+k=0在区间 上有且只有一个实数解,求实数k的取值范围.
上有且只有一个实数解,求实数k的取值范围. ,
, ,设函数
,设函数
 的图象关于直线
的图象关于直线 对称,其中
对称,其中 ,
, 为常数,且
为常数,且 .
.  的最小正周期;
的最小正周期;  的图象经过点
的图象经过点 ,求函数
,求函数 上的取值范围.
上的取值范围.