题目内容
如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD^底面ABCD,PD=DC,点E是PC的中点,作EF^PB交PB于点F,
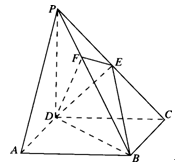
(1)求证:PA//平面EDB;
(2)求证:PB^平面EFD;
(3)求二面角C-PB-D的大小.

(1)求证:PA//平面EDB;
(2)求证:PB^平面EFD;
(3)求二面角C-PB-D的大小.
(1)详见解析;(2)详见解析;(3)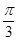 .
.
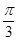 .
.试题分析:(1)证明线面平行,由判定定理,可证明PA与平面EDB内的一条直线平行. 连接AC,交BD于点O,连接EO.即可通过中位线的性质证明EO//PA,从而证明了本题;(2)证明线面垂直,由判定定理,可证明PB与平面EFD内两条相交直线垂直.又题设条件已给出EF^PB,从而只需再找出一条即可.由题意,可以证明DE⊥面PCB,从而DE⊥PB.本题即可得证;(3)由第(2)问,通过垂面法可知∠DFE即为二面角C-PB-D的平面角.又易知DE^EF,再计算各边,从而由三角函数知识可得二面角C-PB-D的平面角为
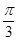 .
.试题解析:(1)证明:连接AC,交BD于点O,连接EO.
可知O为AC的中点,又因为E为PC的中点,
所以EO//PA, 因为EO
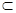 面EDB,PA
面EDB,PA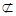 面EDB
面EDB∴PA//平面EDB 4分

(2)证明:∵侧棱PD^底面ABCD,且BC
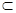 面ABCD
面ABCD∴BC ^PD,又BC⊥CD,PD∩CD="D," ∴BC ^面PCD.因为DE
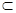 面PCD, ∴BC ^ DE
面PCD, ∴BC ^ DE又PD=DC,点E是PC的中点,可知DE ^PC.由于PC∩BC=C,所以DE⊥面PCB.
∴DE⊥PB 同时EF⊥PB,DE∩EF=E
可得 PB^平面EFD 8分
(3)解:由(2)得PB^平面EFD,且EF
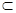 面CPB,DF
面CPB,DF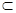 面DPB
面DPB所以∠DFE即为二面角C-PB-D的平面角.设PD=DC=2
在Rt△DEF中,DE^EF,且DE=
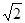 ,PF=
,PF=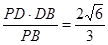 .
.∴sin∠DFE=
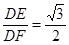 ,因此二面角C-PB-D的平面角为
,因此二面角C-PB-D的平面角为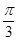 . 12分
. 12分
练习册系列答案
相关题目
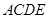 所在的平面垂直于平面
所在的平面垂直于平面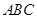 ,
,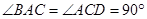 ,
,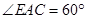 ,
,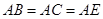 .
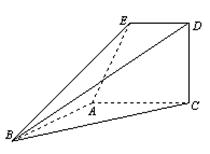
.
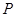 是直线
是直线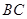 中点,证明
中点,证明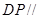 平面
平面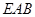 ;
;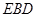 与平面
与平面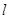 外两点作与直线
外两点作与直线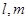 ,平面
,平面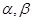 ,且
,且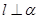 ,
,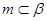 ,给出下列四个命题:
,给出下列四个命题: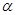 ∥
∥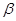 ,则
,则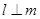 ;
;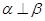 ,则
,则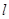 ∥
∥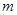 ;
;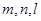 ,两个不重合的平面
,两个不重合的平面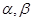 ,有下列命题:
,有下列命题: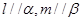 ,且
,且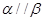 ,则
,则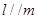
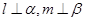 ,且
,且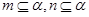 ,
,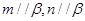 ,则
,则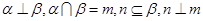 ,则
,则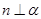
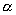 外的两条直线,给出下列
外的两条直线,给出下列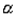 ,则b∥
,则b∥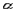 ,则
,则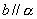 .则所有正确命题的序号是________.
.则所有正确命题的序号是________. 中,
中,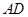 ∥
∥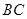 ,
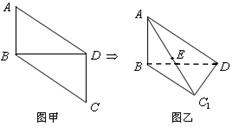
,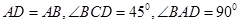 ,将
,将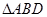 沿
沿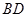 折起,使平面
折起,使平面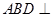 平面
平面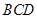 ,构成三棱锥
,构成三棱锥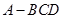 ,则在三棱锥
,则在三棱锥
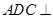 平面
平面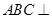 平面
平面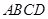 中,
中,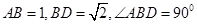 ,将它们沿对角线
,将它们沿对角线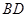 折起,折后的点
折起,折后的点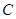 变为
变为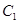 ,且
,且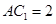 .
.
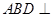 平面
平面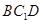 ;
;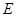 为线段
为线段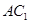 上的一个动点,当线段
上的一个动点,当线段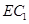 的长为多少时,
的长为多少时,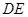 与平面
与平面 ?
?