题目内容
【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,AD∥BC,CD=13,AB=12,BC=10,AD=5,PD=8,点E,F分别是PB,DC的中点. 
(1)求证:EF∥平面PAD;
(2)求EF与平面PDB所成角的正弦值.
【答案】
(1)证明:取CB的中点G,连结DG,因为AD∥BG且AD=BD,
所以四边形ABGD为平行四边形,
所以DG=AB=12,
又因为AB⊥AD,
所以DG⊥AD,
又PD⊥平面ABCD,
故以点D原点建立如图所示的空间直角坐标系.
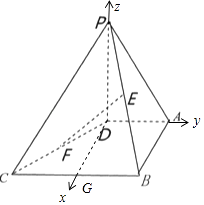
因为BC=10,AD=5,PD=8,
所以有D(0,0,0),P(0,0,8),B(12,5,0),C(12,﹣5,0),
因为E,F分别是PB,DC的中点,
所以E(6,﹣2.5,0),F(6,2.5,4),
因为PD⊥平面ABCD,DG平面ABCD,
所以PD⊥DG,
又因为DG⊥AD,AD∩PD=D,AD,PD平面PAD,
所以DG⊥平面PAD,
所以 ![]() =(12,0,0)为平面PAD的一个法向量,
=(12,0,0)为平面PAD的一个法向量,
又 ![]() =(0,5,4),
=(0,5,4), ![]() =0,
=0,
所以 ![]() ,
,
又EF平面PAD,所以EF∥平面PAD
(2)解:设平面PAD的法向量为 ![]() =(x,y,z),
=(x,y,z),
所以 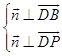 ,即
,即 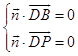 ,即
,即 ![]() ,
,
令x=5,则 ![]() =(5,﹣12,0)
=(5,﹣12,0)
所以EF与平面PDB所成角θ满足:
sinθ= 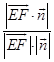 =
= ![]() =
= ![]() ,
,
所以EF与平面PDB所成角的正弦值为 ![]()
【解析】取CB的中点G,连结DG,建立空间直角坐标系:(1) ![]() =(12,0,0)为平面PAD的一个法向量,根据
=(12,0,0)为平面PAD的一个法向量,根据 ![]() ,进而可证EF∥面PAD(2)平面PAD的法向量
,进而可证EF∥面PAD(2)平面PAD的法向量 ![]() =(5,﹣12,0),代和线面夹角公式,可得答案.
=(5,﹣12,0),代和线面夹角公式,可得答案.

 快乐5加2金卷系列答案
快乐5加2金卷系列答案【题目】通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由 ![]() 算得,
算得, ![]() .
.
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
C.有99%以上的把握认为“爱好该项运动与性别有关”
D.有99%以上的把握认为“爱好该项运动与性别无关”