题目内容
【题目】在长方体ABCD-A1B1C1D1中(如图),AD=AA1=1,AB=2,点E是棱AB的中点.
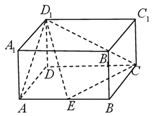
(1)求异面直线AD1与EC所成角的大小;
(2)《九章算术》中,将四个面都是直角三角形的四面体称为鳖臑,试问四面体D1CDE是否为鳖臑?并说明理由.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)取CD中点F,连接AF,则AF∥EC,即∠D1AF为异面直线AD1与EC所成角,解三角形可得△AD1F为等边三角形,从而得到异面直线AD1与EC所成角的大小;
(2)证明DE⊥CE,进一步得到D1E⊥CE,可知四面体D1CDE是鳖臑.
解:(1)取CD中点F,连接AF,则AF∥EC,
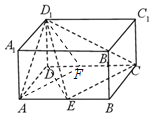
∴∠D1AF为异面直线AD1与EC所成角.
在长方体ABCD-A1B1C1D1中,由AD=AA1=1,AB=2,
得![]()
∴△AD1F为等边三角形,则![]() .
.
∴异面直线AD1与EC所成角的大小为![]() ;
;
(2)连接DE,∵E为AB的中点,∴DE=EC=![]() ,
,
又CD=2,∴DE2+CE2=DC2,得DE⊥CE.
∵D1D⊥底面DEC,则D1D⊥CE,∴CE⊥平面D1DE,得D1E⊥CE.
∴四面体D1CDE的四个面都是直角三角形,
故四面体D1CDE是鳖臑.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
