题目内容
14.已知数列{an}的各项均正数,记A(n)是其前n项的积,B(n)是从第二项开始往后n项的积,C(n)是从第三项开始往后n项的积,n=1,2,….若a1=1,a2=2,且对任意n∈N*,三个数A(n),B(n),C(n)组成等比数列,则数列{an}的通项公式为an=2n-1.分析 由题意易得$\frac{{a}_{n+1}}{{a}_{1}}=\frac{{a}_{n+2}}{{a}_{2}}$,进而可得$\frac{{a}_{n+2}}{{a}_{n+1}}$=2,可得数列{an}是首项为1,公比为2的等比数列,可得通项公式.
解答 解:由题意,对任意n∈N*,三个数A(n),B(n),C(n)组成等比数列,
所以$\frac{{a}_{n+1}}{{a}_{1}}=\frac{{a}_{n+2}}{{a}_{2}}$,
因为a1=1,a2=2,
所以$\frac{{a}_{n+2}}{{a}_{n+1}}$=2,
所以数列{an}是首项为1,公比为2的等比数列,
所以an=2n-1.
故答案为:an=2n-1.
点评 本题考查等比数列的通项公式,属基础题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
5.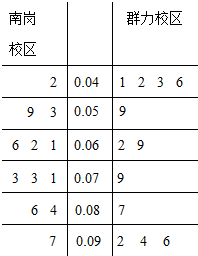 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如图是根据哈尔滨三中学生社团某日早6点至晚9点在南岗、群力两个校区附近的PM2.5监测点统计的数据(单位:毫克/立方米)列出的茎叶图,南岗、群力两个校区浓度的方差较小的是( )
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如图是根据哈尔滨三中学生社团某日早6点至晚9点在南岗、群力两个校区附近的PM2.5监测点统计的数据(单位:毫克/立方米)列出的茎叶图,南岗、群力两个校区浓度的方差较小的是( )
 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如图是根据哈尔滨三中学生社团某日早6点至晚9点在南岗、群力两个校区附近的PM2.5监测点统计的数据(单位:毫克/立方米)列出的茎叶图,南岗、群力两个校区浓度的方差较小的是( )
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如图是根据哈尔滨三中学生社团某日早6点至晚9点在南岗、群力两个校区附近的PM2.5监测点统计的数据(单位:毫克/立方米)列出的茎叶图,南岗、群力两个校区浓度的方差较小的是( )| A. | 南岗校区 | B. | 群力校区 | ||
| C. | 南岗、群力两个校区相等 | D. | 无法确定 |
2.已知复数z=$\frac{1-2i}{3+4i}$(i是虚数单位),则z的共轭复数的虚部是( )
| A. | -$\frac{2}{5}$i | B. | $\frac{2}{5}$i | C. | -$\frac{2}{5}$ | D. | $\frac{2}{5}$ |