题目内容
15.已知集合M={0,1,2,3},N={x|x2-3x<0},则M∩N=( )| A. | {1,2} | B. | {x|x<0} | C. | {x|0<x<3} | D. | {0} |
分析 求出N中不等式的解集确定出N,找出M与N的交集即可.
解答 解:由N中不等式变形得:x(x-3)<0,
解得:0<x<3,即N=(0,3),
∵M={0,1,2,3},
∴M∩N={1,2},
故选:A.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{{1-{a^2}}}=1$(a>0)的离心率为$\sqrt{2}$,则a的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
3.已知实数x、y满足不等式组$\left\{\begin{array}{l}{x-3y+1≤0}\\{x+y-3≥0}\\{x≥0}\end{array}\right.$,则x2+y2的最小值是( )
| A. | $\frac{3\sqrt{2}}{2}$ | B. | $\frac{9}{2}$ | C. | 5 | D. | 9 |
10.在复平面内,复数z=1-2i对应的点的坐标为( )
| A. | (1,2) | B. | (2,1) | C. | (1,-2) | D. | (2,-1) |
20.已知集合A={0,b},B={x∈Z|x2-3x<0},若A∩B≠∅,则b等于( )
| A. | 1 | B. | 2 | C. | 3 | D. | 1或2 |
7.已知i是虚数单位,复数$\frac{1+i}{2-i}$=( )
| A. | $\frac{1}{5}-\frac{3}{5}$i | B. | $\frac{3}{5}+\frac{1}{5}$i | C. | $\frac{1}{3}+\frac{2}{3}$i | D. | $\frac{1}{5}+\frac{3}{5}$i |
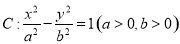 的右焦点为
的右焦点为 ,直线
,直线 与双曲线
与双曲线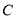 的渐近线在第一象限的交点为
的渐近线在第一象限的交点为 为坐标原点,若
为坐标原点,若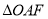 的面积为
的面积为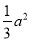 ,则双曲线
,则双曲线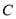 的离心率为( )
的离心率为( ) B.
B.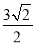
 D.
D.
 ,若
,若 ,则
,则 等于( )
等于( )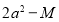 B.
B.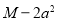
 D.
D.