题目内容
7.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{{1-{a^2}}}=1$(a>0)的离心率为$\sqrt{2}$,则a的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
分析 直接利用双曲线求出半焦距,利用离心率求出a即可.
解答 解:双曲线$\frac{x^2}{a^2}-\frac{y^2}{{1-{a^2}}}=1$,可得c=1,
双曲线的离心率为:$\sqrt{2}$,
∴$\frac{c}{a}=\sqrt{2}$,解得a=$\frac{\sqrt{2}}{2}$.
故选:B.
点评 本题考查双曲线的离心率的求法,双曲线的简单性质的应用.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
15.下列命题中,真命题的是( )
| A. | ?x0∈R,ex0≤0 | B. | ?x∈R,2x>x2 | ||
| C. | “若x>3,则x>2”的否命题 | D. | “x2≠1”是“x≠1”的充分不必要条件 |
16.执行如图的程序框图,若输出k的值为6,则判断框内可填入的条件是( )
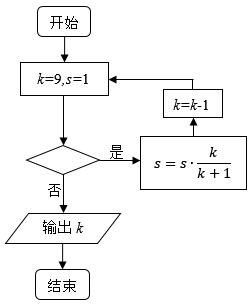

| A. | s$>\frac{4}{5}$ | B. | s$>\frac{7}{10}$ | C. | s$>\frac{3}{5}$ | D. | s$>\frac{1}{2}$ |
15.已知集合M={0,1,2,3},N={x|x2-3x<0},则M∩N=( )
| A. | {1,2} | B. | {x|x<0} | C. | {x|0<x<3} | D. | {0} |
 中,
中,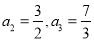 ,且数列
,且数列 是等比数列,则
是等比数列,则 ___________.
___________.