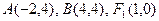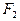题目内容
已知抛物线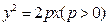 的焦点为
的焦点为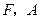 是抛物线上横坐标为
是抛物线上横坐标为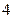 ,且位于
,且位于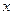 轴上方的点,
轴上方的点,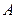 到抛物线准线的距离等于
到抛物线准线的距离等于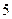 .过
.过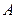 作
作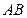 垂直于
垂直于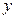 轴,垂足为
轴,垂足为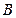 ,
,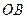 的中点为
的中点为 .
.
(1) 求抛物线方程;
求抛物线方程;
(2) 过 作
作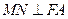 ,垂足为
,垂足为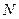 ,求点
,求点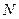 的坐标;
的坐标;
(3) 以 为圆心,
为圆心,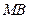 为半径作圆
为半径作圆 .当
.当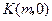 是
是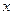 轴上一动点
轴上一动点
时,讨论直线 与圆
与圆 的位置关系.
的位置关系.
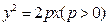 的焦点为
的焦点为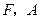 是抛物线上横坐标为
是抛物线上横坐标为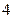 ,且位于
,且位于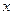 轴上方的点,
轴上方的点,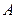 到抛物线准线的距离等于
到抛物线准线的距离等于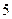 .过
.过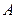 作
作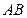 垂直于
垂直于 轴,垂足为
轴,垂足为 ,
, 的中点为
的中点为 .
.(1)
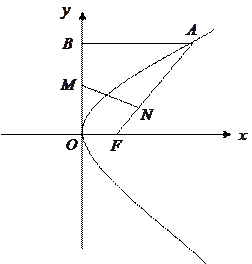 求抛物线方程;
求抛物线方程;(2) 过
 作
作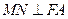 ,垂足为
,垂足为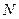 ,求点
,求点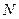 的坐标;
的坐标;(3) 以
 为圆心,
为圆心,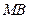 为半径作圆
为半径作圆 .当
.当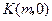 是
是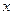 轴上一动点
轴上一动点时,讨论直线
 与圆
与圆 的位置关系.
的位置关系.(1)抛物线方程为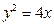 . 2)
. 2) .
.
(4) 当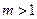 时,直线
时,直线 与圆
与圆 相离;当
相离;当 时,直线
时,直线 到圆
到圆 相切;
相切;
当 时,直线
时,直线 与圆
与圆 相交.
相交.
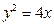 . 2)
. 2) .
.(4) 当
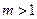 时,直线
时,直线 与圆
与圆 相离;当
相离;当 时,直线
时,直线 到圆
到圆 相切;
相切;当
 时,直线
时,直线 与圆
与圆 相交.
相交.(1)抛物线 的准线为
的准线为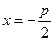 ,于是,
,于是,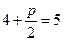 .
.
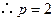 ,
, 抛物线方程为
抛物线方程为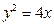 .
.
(2) 点
点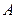 的坐标是
的坐标是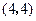 .由题意得
.由题意得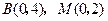 .
.
又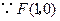 ,
, ;
;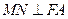 ,
,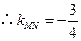 ,则
,则 的方程为
的方程为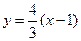 ,
,
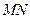 的方程为
的方程为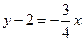 ,解方程组
,解方程组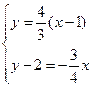 ,得
,得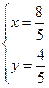 ,
, .
.
(3)由题意得,圆 的圆心是点
的圆心是点 ,半径为
,半径为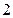 .
.
当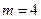 时,直线
时,直线 的方程为
的方程为 ,此时,直线
,此时,直线 与圆
与圆 相离,
相离,
当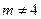 时,直线
时,直线 的方程为
的方程为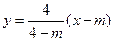 ,即为
,即为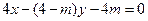 ,
,
圆心 到直线
到直线 的距离
的距离 .
.
令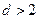 ,解得
,解得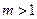 .
. 当
当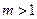 时,直线
时,直线 与圆
与圆 相离;
相离;
当 时,直线
时,直线 到圆
到圆 相切;当
相切;当 时,直线
时,直线 与圆
与圆 相交.
相交.
 的准线为
的准线为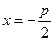 ,于是,
,于是,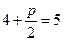 .
.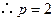 ,
, 抛物线方程为
抛物线方程为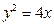 .
.(2)
 点
点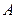 的坐标是
的坐标是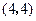 .由题意得
.由题意得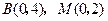 .
.又
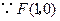 ,
, ;
;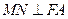 ,
,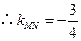 ,则
,则 的方程为
的方程为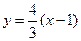 ,
,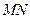 的方程为
的方程为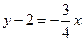 ,解方程组
,解方程组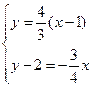 ,得
,得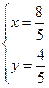 ,
, .
.(3)由题意得,圆
 的圆心是点
的圆心是点 ,半径为
,半径为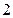 .
.当
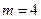 时,直线
时,直线 的方程为
的方程为 ,此时,直线
,此时,直线 与圆
与圆 相离,
相离,当
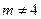 时,直线
时,直线 的方程为
的方程为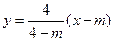 ,即为
,即为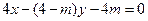 ,
,圆心
 到直线
到直线 的距离
的距离 .
.令
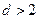 ,解得
,解得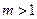 .
. 当
当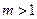 时,直线
时,直线 与圆
与圆 相离;
相离;当
 时,直线
时,直线 到圆
到圆 相切;当
相切;当 时,直线
时,直线 与圆
与圆 相交.
相交.
练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 与曲线
与曲线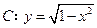 有两个公共点,求实数
有两个公共点,求实数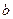 的取值范围.
的取值范围. 交双曲线
交双曲线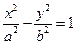 及其渐近线于
及其渐近线于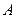 ,
, ,
, ,
, 四点,求证:
四点,求证: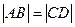 .
.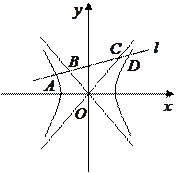
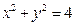 外一点
外一点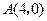 ,作圆的割线,求割线被圆截得的弦的中点的轨迹方程.
,作圆的割线,求割线被圆截得的弦的中点的轨迹方程.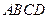 中,
中,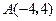 ,
,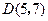 ,中心
,中心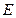 在第一象限内,且与
在第一象限内,且与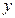 轴的距离为一个单位,动点
轴的距离为一个单位,动点 沿矩形一边
沿矩形一边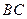 运动,求
运动,求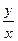 的取值范围.
的取值范围. 的顶点在原点,焦点在
的顶点在原点,焦点在 轴上,斜率为
轴上,斜率为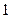 的直线交
的直线交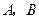 两点,若
两点,若 ,且以
,且以 为直径的圆经过原点
为直径的圆经过原点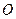 ,求直线
,求直线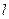 和抛物线
和抛物线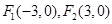 ,一条渐近线方程为
,一条渐近线方程为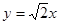 ,则该双曲线的方程为________________
,则该双曲线的方程为________________ 的顶点和准线.
的顶点和准线. 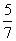 ,求点P到x轴的距离;
,求点P到x轴的距离;