题目内容
1．在平面内，曲线C上存在点P，使点P到点A（3，0），B（-3，0）的距离之和为10，则称曲线C为“有用曲线”．以下曲线不是“有用曲线”的是（ ）| A． | x+y=5 | B． | x2+y2=9 | C． | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1 | D． | x2=16y |
分析 由点P到点A（3，0），B（-3，0）的距离之和为10，可得$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}=1$．分别与A，B，C，D中的方程联立，判断是否有解即可得出．
解答 解：由点P到点A（3，0），B（-3，0）的距离之和为10，可得$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}=1$．
A．联立$\left\{\begin{array}{l}{x+y=5}\\{\frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}=1}\end{array}\right.$，化为41x2-250x+225=0，△=2502-41000＞0，因此曲线x+y=5上存在点P满足条件，∴是“有用曲线”，正确；
同理可判断C，D给出的切线是“有用曲线”，而B给出的曲线不是“有用曲线”．
故选：B．
点评 本题考查了椭圆的定义、两点之间的距离公式、曲线的交点，考查了推理能力与技能数列，属于中档题．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
12．（1）证明：垂直同一平面的两直线平行；
（2）已知l1⊥平面α，l2⊥平面α，且l1，l2与α的交点分别为O1，O2，A、B分别在l1，l2上，且AO1=3，BO2=1，O1O2=2，求|AB|．
（2）已知l1⊥平面α，l2⊥平面α，且l1，l2与α的交点分别为O1，O2，A、B分别在l1，l2上，且AO1=3，BO2=1，O1O2=2，求|AB|．
16．若把函数y=3cos（2x+$\frac{π}{3}$）的图象上的所有点向右平移m（m＞0）个单位长度后，所得到的图象关于y轴对称，则m的最小值是（ ）
| A． | $\frac{2}{3}π$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{6}$ | D． | $\frac{π}{12}$ |
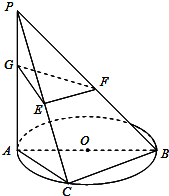如图，已知PA⊥⊙O所在的平面，AB是⊙O的直径，AB=2，C是⊙O上一点，且AC=BC，∠PCA=45°，E是PC的中点，F是PB的中点，G为线段PA上（除点P外）的一个动点．
10．“0≤m≤1”是“函数f（x）=sinx+m-1有零点”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |