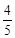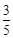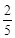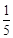题目内容
设数列 的前n项和为
的前n项和为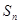 ,已知
,已知 ,
,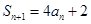
(1)设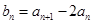 ,证明数列
,证明数列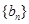 是等比数列 (2)求数列
是等比数列 (2)求数列 的前
的前 项和
项和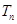
 的前n项和为
的前n项和为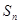 ,已知
,已知 ,
,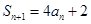
(1)设
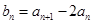 ,证明数列
,证明数列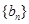 是等比数列 (2)求数列
是等比数列 (2)求数列 的前
的前 项和
项和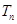
(1)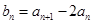
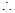
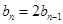 ,
,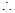
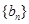 }是以
}是以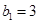 为首项、2为公比的等比数列
为首项、2为公比的等比数列
(2)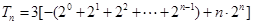
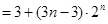 .
.
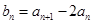
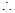
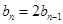 ,
,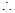
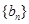 }是以
}是以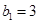 为首项、2为公比的等比数列
为首项、2为公比的等比数列 (2)
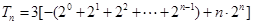
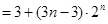 .
.试题分析:
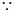
 ,当
,当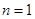 时有
时有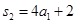 即
即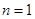
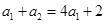
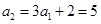 ,
,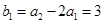 ……2分
……2分由
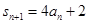 ① 则当
① 则当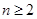 时,有
时,有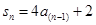 ②
②②-①得:
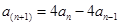
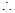
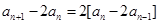
又
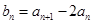
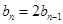
 }是以
}是以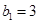 为首项、2为公比的等比数列 4分
为首项、2为公比的等比数列 4分(2)由(1)可得:
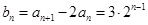 6分
6分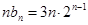

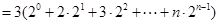 ③
③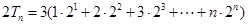 ④ 8分
④ 8分④-③得:
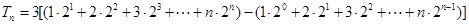
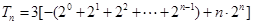 10分
10分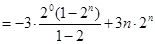
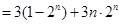
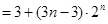 12分
12分点评:中档题,为研究数列的求和问题,先研究数列的通项公式,已选择合适的求和方法。“分组求和法”“裂项相消法”“错位相减法”是高考经常考查的数列求和方法。

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
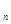 是公差不为0的等差数列
是公差不为0的等差数列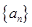 的前
的前 项和,且
项和,且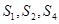 成等比数列。
成等比数列。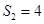 ,求
,求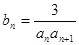 ,
,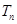 是数列
是数列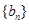 的前
的前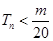 对所有
对所有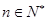 都成立的最小正整数
都成立的最小正整数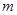 。
。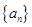 的首项
的首项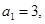 前
前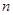 项和为
项和为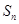 ,且
,且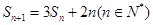 ,
,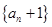 是否成等比数列?并求出数列
是否成等比数列?并求出数列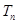 为数列
为数列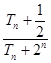 的最小值.
的最小值.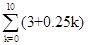 =
= 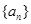 的前
的前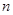 项和为
项和为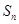 ,
,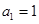 ,
,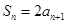 ,,则
,,则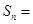 .
.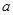
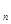 },(n∈N
},(n∈N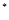 )是等差数列,则有数列b
)是等差数列,则有数列b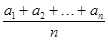 (n∈N
(n∈N 满足
满足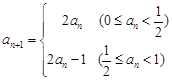 ,若
,若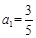 ,则
,则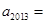 ( )
( )