题目内容
8.已知{an}是各项项都为正数的数列,其前n项和为Sn,且满足2anSn-an2=1(Ⅰ)证明{Sn2}是等差数列,并求数列{an}的通项公式;
(Ⅱ)求数列{Sn2xn-1}的前n项和Tn.
分析 (Ⅰ)把an=Sn-Sn-1(n≥2)代入2anSn-an2=1,整理后即可证明{Sn2}是等差数列,求其通项公式后再由an=Sn-Sn-1(n≥2)求数列{an}的通项公式;
(Ⅱ)把Sn2=n代入Sn2xn-1,对x分类后借助于等比数列的前n项和求得数列{Sn2xn-1}的前n项和Tn.
解答 (Ⅰ)证明:∵2anSn-an2=1,
∴当n≥2时,2(Sn-Sn-1)Sn-$({S}_{n}-{S}_{n-1})^{2}=1$,
整理得,${{S}_{n}}^{2}-{{S}_{n-1}}^{2}=1$(n≥2),
又${{S}_{1}}^{2}$=1,
∴数列{Sn2}为首项和公差都是1的等差数列.
∴${{S}_{n}}^{2}=n$,
又Sn>0,∴Sn=$\sqrt{n}$.
∴n≥2时,an=Sn-Sn-1=$\sqrt{n}-\sqrt{n-1}$,又a1=S1=1适合此式.
∴数列{an}的通项公式为an=$\sqrt{n}-\sqrt{n-1}$;
(Ⅱ)解:Sn2xn-1=n•xn-1.
当x=0时,Tn=0;
当x=1时,Tn=1+2+…+n=$\frac{n(n+1)}{2}$;
当x≠0且x≠1时,
Tn=1•x0+2•x1+3•x2+…+n•xn-1.
$x{T}_{n}=1•{x}^{1}+2•{x}^{2}+3•{x}^{3}+…+(n-1){x}^{n-1}+n{x}^{n}$.
两式作差得:$(1-x){T}_{n}=1+x+{x}^{2}+…+{x}^{n-1}-n{x}^{n}$=$\frac{1-{x}^{n}}{1-x}-n{x}^{n}$.
∴${T}_{n}=\frac{1-{x}^{n}}{(1-x)^{2}}-\frac{n{x}^{n}}{1-x}$.
综上,当x=0时,Tn=0;
当x=1时,Tn=$\frac{n(n+1)}{2}$;
当x≠0且x≠1时,${T}_{n}=\frac{1-{x}^{n}}{(1-x)^{2}}-\frac{n{x}^{n}}{1-x}$.
点评 本题考查数列递推式,考查了等差关系的确定,训练了等比数列前n项和的求法,体现了分类讨论的数学思想方法,是中档题.

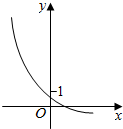
| A. | a>1,b>1 | B. | a>1,0<b<1 | C. | 0<a<1,b>1 | D. | 0<a<1,0<b<1 |
| A. | $2\sqrt{5}-3$ | B. | $3\sqrt{5}-2\sqrt{2}$ | C. | $3\sqrt{2}+2$ | D. | $2\sqrt{5}+\sqrt{2}$ |
| A. | $f_a^b(f(x)-g(x))dx$ | B. | $f_a^b(g(x)-f(x))dx$ | C. | $f_a^b|{f(x)-g(x)}|dx$ | D. | $|{f_a^b(f(x)-g(x))dx}|$ |