题目内容
在极坐标系中,圆 :
: 和直线
和直线 相交于
相交于 、
、 两点,求线段
两点,求线段 的长
的长
【解析】本试题主要考查了极坐标系与参数方程的运用。先将圆的极坐标方程圆 :
: 即
即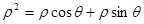 化为直角坐标方程即
化为直角坐标方程即 
然后利用直线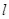
 即
即 ,得到圆心到直线的距离
,得到圆心到直线的距离 ,从而利用勾股定理求解弦长AB。
,从而利用勾股定理求解弦长AB。
解:分别将圆 和直线
和直线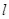 的极坐标方程化为直角坐标方程:
的极坐标方程化为直角坐标方程:
圆 :
: 即
即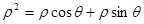 即
即  ,
,
即 , ∴ 圆心
, ∴ 圆心 ,
, ---------3分
---------3分
直线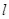
 即
即 , ------6分
, ------6分
则圆心 到直线
到直线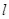 的距离
的距离 ,----------8分
,----------8分
则 即所求弦长为
即所求弦长为
【答案】
弦长为

练习册系列答案
相关题目
 A、选修4-1:几何证明选讲
A、选修4-1:几何证明选讲