题目内容
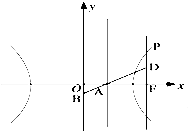
如图,已知双曲线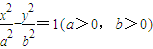 ,其右准线交x轴于点A,双曲线虚轴的下端点为B.过双曲线的右焦点F(c,0)作垂直于x轴的直线交双曲线于点P,若点D满足
,其右准线交x轴于点A,双曲线虚轴的下端点为B.过双曲线的右焦点F(c,0)作垂直于x轴的直线交双曲线于点P,若点D满足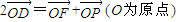 ,
,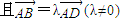 .
.(1)求双曲线的离心率;
(2)若a=2,过点B作直线l分别交双曲线的左支、右支于M、N两点,且△OMN的面积S△OMN=
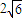 ,求l的方程.
,求l的方程.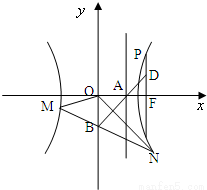
【答案】分析:(1)欲求双曲线的离心率,只需找到含a,c的齐次式,由已知,易求P点坐标,根据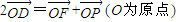 ,可判断D点为FP的中点,再根据
,可判断D点为FP的中点,再根据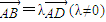 可找到a,b的关系,进而转化为含a,c的等式,即可求出离心率e的值.
可找到a,b的关系,进而转化为含a,c的等式,即可求出离心率e的值.
(2)当a=2时,根据(1)中所求离心率,可求出b的值,进而求出双曲线方程,根据直线MN过B点,设出直线MN的方程,与双曲线方程联立,解出x1+x2,x1x2,△OMN被y轴分成两个三角形,分别求出面积,再相加,即为△OMN的面积,让其等于题目中所给的值,可得到关于直线l的斜率k的方程,解出k即可.
解答: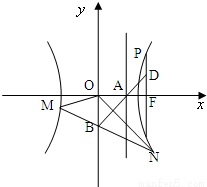 解:(1)∵B(0,-b)
解:(1)∵B(0,-b)
∵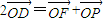 ,即D为线段FP的中点.,
,即D为线段FP的中点.,
∴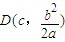
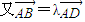 ,即A、B、D共线.
,即A、B、D共线.
而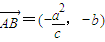 ,
,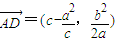 ,
,
∴ ,得a=2b,
,得a=2b,
∴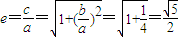
(2)∵a=2,而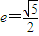 ,∴b2=1,
,∴b2=1,
故双曲线的方程为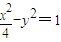 …①
…①
∴B、的坐标为(0,-1)
设l的方程为y=kx-1…②
②代入①得(1-4k2)x2+8kx-8=0
由题意得: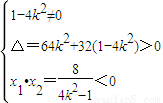 得:
得: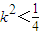
设M、N的坐标分别为(x1,y1)、(x2,y2)
则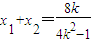
而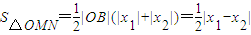 =
=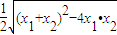 =
=
整理得24k4-11k2+1=0,解得: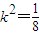 或
或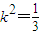 (舍去)
(舍去)
∴所求l的方程为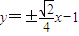
点评:本题主要考查了双曲线离心率的求法,以及直线与 双曲线位置关系的应用.
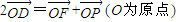 ,可判断D点为FP的中点,再根据
,可判断D点为FP的中点,再根据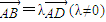 可找到a,b的关系,进而转化为含a,c的等式,即可求出离心率e的值.
可找到a,b的关系,进而转化为含a,c的等式,即可求出离心率e的值.(2)当a=2时,根据(1)中所求离心率,可求出b的值,进而求出双曲线方程,根据直线MN过B点,设出直线MN的方程,与双曲线方程联立,解出x1+x2,x1x2,△OMN被y轴分成两个三角形,分别求出面积,再相加,即为△OMN的面积,让其等于题目中所给的值,可得到关于直线l的斜率k的方程,解出k即可.
解答:
 解:(1)∵B(0,-b)
解:(1)∵B(0,-b)
∵
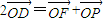 ,即D为线段FP的中点.,
,即D为线段FP的中点.,∴
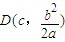
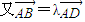 ,即A、B、D共线.
,即A、B、D共线.而
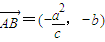 ,
,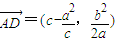 ,
,∴
 ,得a=2b,
,得a=2b,∴
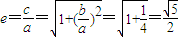
(2)∵a=2,而
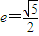 ,∴b2=1,
,∴b2=1,故双曲线的方程为
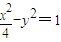 …①
…①∴B、的坐标为(0,-1)
设l的方程为y=kx-1…②
②代入①得(1-4k2)x2+8kx-8=0
由题意得:
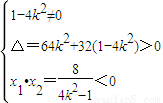 得:
得: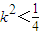
设M、N的坐标分别为(x1,y1)、(x2,y2)
则
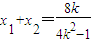
而
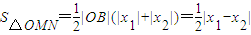 =
=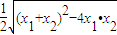 =
=
整理得24k4-11k2+1=0,解得:
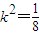 或
或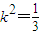 (舍去)
(舍去)∴所求l的方程为
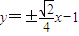
点评:本题主要考查了双曲线离心率的求法,以及直线与 双曲线位置关系的应用.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 如图,已知双曲线
如图,已知双曲线 如图,已知双曲线C1:
如图,已知双曲线C1: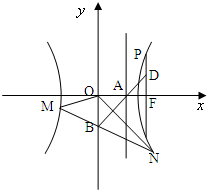 (2008•湖北模拟)如图,已知双曲线
(2008•湖北模拟)如图,已知双曲线