题目内容
【题目】如图，在矩形ABCD中，|AB|=4，|AD|=2，O为AB中点，P，Q分别是AD和CD上的点，且满足① 
= 
，②直线AQ与BP的交点在椭圆E： 
+ 
=1（a＞b＞0）上．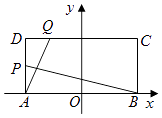
（Ⅰ）求椭圆E的方程；
（Ⅱ）设R为椭圆E的右顶点，M为椭圆E第一象限部分上一点，作MN垂直于y轴，垂足为N，求梯形ORMN面积的最大值．
【答案】解：（Ⅰ）设AQ于BP交点C为（x，y），P（﹣2，y1），Q（x1 ， 2），
由题可知， 
，
从而有 
，整理得 
，即为椭圆方程，
椭圆E的方程 ；
（Ⅱ）R（2，0），设M（x0 ， y0），有 
，
从而所求梯形面积 
= 
，
令t=2+x0 ， 2＜t＜4， 
，
令u=4t3﹣t4 ， u'=12t2﹣4t3=4t2（3﹣t），
当t∈（2，3）时，u=4t3﹣t4单调递增，
当t∈（3，4）时，u=4t3﹣t4单调递减，则当t=3时S取最大值 
，
梯形ORMN面积的最大值
【解析】（Ⅰ）由题可知， ，整理即可求得椭圆E的方程；（Ⅱ）由 ，则梯形面积 = ，t=2+x0 ， 2＜t＜4， ，根据函数的单调性即可求得梯形ORMN面积的最大值．
【题目】某市对大学生毕业后自主创业人员给予小额贷款补贴，贷款期限分为6个月、12个月、18个月、24个月、36个月五种，对于这五种期限的贷款政府分别补贴200元、300元、300元、400元、400元，从2016年享受此项政策的自主创业人员中抽取了100人进行调查统计，选取贷款期限的频数如表：
贷款期限 | 6个月 | 12个月 | 18个月 | 24个月 | 36个月 |
频数 | 20 | 40 | 20 | 10 | 10 |
以上表中各种贷款期限的频数作为2017年自主创业人员选择各种贷款期限的概率．
（Ⅰ）某大学2017年毕业生中共有3人准备申报此项贷款，计算其中恰有两人选择贷款期限为12个月的概率；
（Ⅱ）设给某享受此项政策的自主创业人员补贴为X元，写出X的分布列；该市政府要做预算，若预计2017年全市有600人申报此项贷款，则估计2017年该市共要补贴多少万元．
