题目内容
【题目】[选修4-4:坐标系与参数方程]
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以直角坐标系的原点
为参数),在以直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,求
两点,求![]() 的面积.
的面积.
【答案】(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]()
【解析】试题分析:(Ⅰ)由![]() ,
, ![]() 可得曲线
可得曲线![]() 的直角坐标方程,直线消去参数
的直角坐标方程,直线消去参数![]() 即可;
即可;
(Ⅱ)将直线![]() 的参数方程化为
的参数方程化为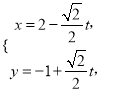 (t为参数),与抛物线联立得
(t为参数),与抛物线联立得![]() ,设
,设![]() 两点对应的参数分别为
两点对应的参数分别为![]() ,
, ![]() ,原点到直线
,原点到直线![]() 的距离
的距离![]() 即可得解.
即可得解.
试题解析:
(Ⅰ)由曲线![]() 的极坐标方程为
的极坐标方程为![]() ,得
,得![]() ,
,
所以曲线![]() 的直角坐标方程是
的直角坐标方程是![]() .
.
由直线![]() 的参数方程为
的参数方程为![]() (t为参数),得直线
(t为参数),得直线![]() 的普通方程
的普通方程![]() .
.
(Ⅱ)由直线![]() 的参数方程为
的参数方程为![]() (t为参数),得
(t为参数),得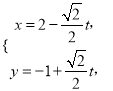 (t为参数),
(t为参数),
代入![]() ,得
,得![]() ,
,
设![]() 两点对应的参数分别为
两点对应的参数分别为![]() ,
,
则![]() ,
,
所以![]() ,
,
因为原点到直线![]() 的距离
的距离![]() ,
,
所以![]() .
.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案【题目】为了提高生产效益,某企业引进了一批新的生产设备,为了解设备生产产品的质量情况,分别从新、旧设备所生产的产品中,各随机抽取100件产品进行质量检测,所有产品质量指标值均在![]() 以内,规定质量指标值大于30的产品为优质品,质量指标值在
以内,规定质量指标值大于30的产品为优质品,质量指标值在![]() 的产品为合格品,旧设备所生产的产品质量指标值如频率分布直方图所示,新设备所生产的产品质量指标值如频数分布表所示.
的产品为合格品,旧设备所生产的产品质量指标值如频率分布直方图所示,新设备所生产的产品质量指标值如频数分布表所示.
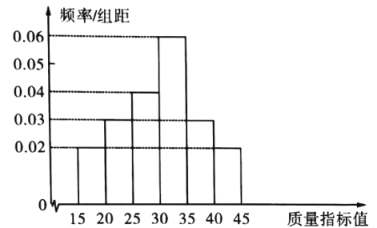
质量指标值 | 频数 |
| 2 |
| 8 |
| 20 |
| 30 |
| 25 |
| 15 |
合计 | 100 |
(1)请分别估计新、旧设备所生产的产品的优质品率.
(2)优质品率是衡量一台设备性能高低的重要指标,优质品率越高说明设备的性能越高,根据已知图表数据填写下面列联表(单位:件),并判断是否有![]() 的把握认为“产品质量高于新设备有关”.
的把握认为“产品质量高于新设备有关”.
非优质品 | 优质品 | 合计 | |
新设备产品 | |||
旧设备产品 | |||
合计 |
附:
P( | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
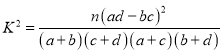 ,其中
,其中![]() .
.
(3)已知每件产品的纯利润y(单位:元)与产品质量指标值t的关系式为![]() 若每台新设备每天可以生产1000件产品,买一台新设备需要80万元,请估计至少需要生产多少天方可以收回设备成本.
若每台新设备每天可以生产1000件产品,买一台新设备需要80万元,请估计至少需要生产多少天方可以收回设备成本.
【题目】自由购是一种通过自助结算购物的形式.某大型超市为调查顾客自由购的使用情况,随机抽取了100人,调查结果整理如下:
20以下 | [20,30) | [30,40) | [40,50) | [50,60) | [60,70] | 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(1)现随机抽取1名顾客,试估计该顾客年龄在[30,50)且未使用自由购的概率;
(2)从被抽取的年龄在[50,70]使用的自由购顾客中,随机抽取2人进一步了解情况,求这2人年龄都在[50,60)的概率;
(3)为鼓励顾客使用自由购,该超市拟对使用自由购顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋?


