题目内容
7.已知平面向量$\overrightarrow{a}$、$\overrightarrow{b}$,|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=$\sqrt{3}$,且|2$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{7}$,则向量$\overrightarrow{a}$与向量$\overrightarrow{a}$+$\overrightarrow{b}$的夹角为$\frac{π}{3}$.分析 由题意可得$\overrightarrow{a}$⊥$\overrightarrow{b}$,由平行四边形法则结合图象可得.
解答 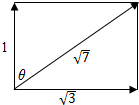 解:∵|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=$\sqrt{3}$,且|2$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{7}$,
解:∵|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=$\sqrt{3}$,且|2$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{7}$,
∴|2$\overrightarrow{a}$+$\overrightarrow{b}$|2=7,∴4${\overrightarrow{a}}^{2}$+4$\overrightarrow{a}•\overrightarrow{b}$+${\overrightarrow{b}}^{2}$=7,
∴4×1+4$\overrightarrow{a}•\overrightarrow{b}$+3=7,
∴$\overrightarrow{a}•\overrightarrow{b}$=0,∴$\overrightarrow{a}$⊥$\overrightarrow{b}$,
设向量$\overrightarrow{a}$与向量$\overrightarrow{a}$+$\overrightarrow{b}$的夹角为θ
结合平行四边形法则可得tanθ=$\sqrt{3}$,
∴θ=$\frac{π}{3}$
故答案为:$\frac{π}{3}$
点评 本题考查数量积和向量的夹角,数形结合是解决问题的关键,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.已知两个相关变量的统计数据如表:
求两变量的线性回归方程.
参考公式:b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\overline{a}$=$\overline{y}$-b$\overline{x}$.
| x | 2 | 3 | 4 | 5 | 6 |
| y | 11 | 15 | 19 | 26 | 29 |
参考公式:b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\overline{a}$=$\overline{y}$-b$\overline{x}$.
18.某科研部门现有男技术员45人,女技术员15人,为研发某新产品的需要,科研部门按照分层抽样的方法组建了一个由四人组成的新产品研发小组.
(1)求每一个技术员被抽到的概率及该新产品研发小组中男、女技术员的人数;
(2)一年后研发小组决定选两名研发的技术员对该项研发产品进行检验,方法是先从研发小组中选一人进行检验,该技术员检验结束后,再从研发小组内剩下的三名技术员中选一人进行检验,若两名技术员检验得到的数据如下:
求先后被选出的两名技术员中恰有一名女技术员的概率;
请问哪位技术员检验更稳定?并说明理由.
(1)求每一个技术员被抽到的概率及该新产品研发小组中男、女技术员的人数;
(2)一年后研发小组决定选两名研发的技术员对该项研发产品进行检验,方法是先从研发小组中选一人进行检验,该技术员检验结束后,再从研发小组内剩下的三名技术员中选一人进行检验,若两名技术员检验得到的数据如下:
| 第一次被抽到进行检验的技术员 | 58 | 53 | 87 | 62 | 78 | 70 | 82 |
| 第二次被抽到进行检验的技术员 | 64 | 61 | 78 | 66 | 74 | 71 | 76 |
请问哪位技术员检验更稳定?并说明理由.
15.在等差数列{an}中,若a4+a9+a14=36,则2a10-a11=( )
| A. | 6 | B. | 12 | C. | 24 | D. | 36 |
19.设O为△ABC的外心,且$\overrightarrow{OA}+\overrightarrow{OB}+\sqrt{3}\overrightarrow{OC}=\overrightarrow 0$,则△ABC的内角C=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |