题目内容
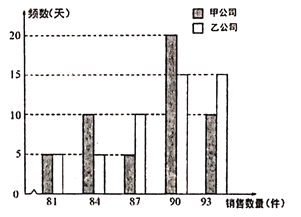
【题目】某工厂生产了一批零件,从中随机抽取100个作为样本,测出它们的长度(单位:厘米),按数据分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 5组,得到如图所示的频率分布直方图.以这100个零件的长度在各组的频率代替整批零件长度在该组的概率.
5组,得到如图所示的频率分布直方图.以这100个零件的长度在各组的频率代替整批零件长度在该组的概率.
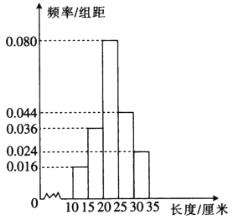
(1)估计该工厂生产的这批零件长度的平均值(同一组中的每个数据用该组区间的中点值代替);
(2)规定零件长度在区间![]() 内的零件为优等品,从这批零件中随机抽取3个,记抽到优等品的个数为X,求X的分布列和数学期望.
内的零件为优等品,从这批零件中随机抽取3个,记抽到优等品的个数为X,求X的分布列和数学期望.
【答案】(1)![]() ;(2)分布列见解析;期望为
;(2)分布列见解析;期望为![]() .
.
【解析】
(1)根据频率分布直方图可得各组频率,然后结合已知进行求解即可;
(2)先求出抽到一个优等品的概率,然后结合二项分布的性质进行求解即可.
解:(1)由频率分布直方图可得各组频率依次为![]() ,
,
则这批零件长度的平均值为
![]() .
.
(2)由题意可得,抽到一个优等品的概率为![]() ,
,
X的可能取值为![]() ,因此X
,因此X![]() ,
,
所以![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
则X的分布列为
X | 0 | 1 | 2 | 3 |
P | 0.008 | 0.096 | 0.384 | 0.512 |
故![]() .
.
(或者![]() )
)

练习册系列答案
相关题目