Question

17．已知点F（1，0），圆E：（x+1）²+y²=8，点P是圆E上任意一点，线段PF的垂直平分线和半径PE相交于Q．求动点Q的轨迹C的方程．

Answer 1

分析 连结QF，根据题意，|QP|=|QF|，则|QE|+|QF|=|QE|+|QP|=4＞|EF|，故Q的轨迹Γ是以E，F为焦点，长轴长为2$\sqrt{2}$的椭圆，从而可求动点Q的轨迹Γ的方程．

解答 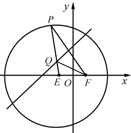解：连结QF，根据题意，|QP|=|QF|，
则|QE|+|QF|=|QE|+|QP|=2$\sqrt{2}$＞|EF|，
故Q的轨迹Γ是以E，F为焦点，长轴长为2$\sqrt{2}$的椭圆，a=$\sqrt{2}$，c=1，
所以b=1，
所以点Q的轨迹Γ的方程为$\frac{{x}^{2}}{2}+{y}^{2}=1$．

点评 本题考查椭圆的定义与方程，考查学生分析解决问题的能力，属于中档题，确定Q的轨迹Γ是以E，F为焦点，长轴长为2$\sqrt{2}$的椭圆是关键．