题目内容
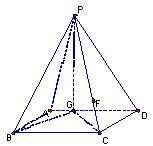
(08年莆田四中二模理)(12分)已知,如图四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() ,垂足
,垂足![]() 在
在![]() 上,且
上,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点.
的中点.
(1)求异面直线![]() 与
与![]() 所成的角;
所成的角;
(2)求点![]() 到平面
到平面![]() 的距离;
的距离;
(3)若![]() 点是棱
点是棱![]() 上一点,且
上一点,且![]() ,求
,求![]() 的值.
的值.

解析:解法一:(1)在平面![]() 内,过
内,过![]() 点作
点作![]() 交
交![]() 于
于![]() ,连结
,连结![]() ,
,
则![]() (或其补角)就是异面直线
(或其补角)就是异面直线![]() 与
与![]() 所成的角.
所成的角.
在![]() 中,
中,![]() ,
,![]()
由余弦定理得,![]() =
=![]()
∴异面直线![]() 与
与![]() 所成的角为arccos
所成的角为arccos![]()
(2)∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ∴平面
∴平面![]() ⊥平面
⊥平面![]()
在平面![]() 内,过
内,过![]() 作
作![]() ,交
,交![]() 延长线于
延长线于![]() ,则
,则![]() ⊥平面
⊥平面![]()
∴![]() 的长就是点
的长就是点![]() 到平面
到平面![]() 的距离
的距离![]()
在![]() ,
,![]() ∴点
∴点![]() 到平面
到平面![]() 的距离为
的距离为![]()
(3)在平面![]() 内,过
内,过![]() 作
作![]() ,
,![]() 为垂足,连结
为垂足,连结![]() ,又因为
,又因为![]()
∴![]() 平面
平面![]() , ∴
, ∴![]()
由平面![]() ⊥平面
⊥平面![]() ,∴
,∴![]() ⊥平面
⊥平面![]() ∴
∴![]()
由![]() 得:
得:![]()
![]()
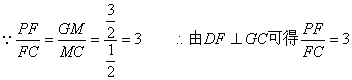
解法二:(1)由已知![]() ∴
∴![]()
如图所示,以G点为原点建立空间直角坐标系o―xyz,则
![]() ,
,![]() ,
,![]() 故
故![]()
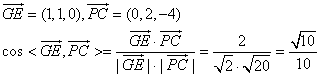
∴异面直线![]() 与
与![]() 所成的角为arccos
所成的角为arccos![]() 4分
4分
(2)平面PBG的单位法向量![]()
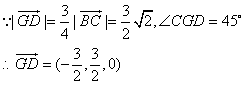
∴点![]() 到平面
到平面![]() 的距离为
的距离为![]() ------------- 8分
------------- 8分
(3)设![]()
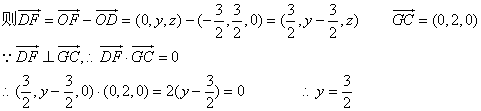
在平面![]() 内过
内过![]() 点作
点作![]() ,
,![]() 为垂足,则
为垂足,则![]()
![]() ------------- 12分
------------- 12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 其中
其中