题目内容
3.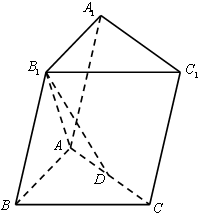 如图,在三棱柱ABC-A1B1C1中,AB1=B1B=BA=BC,∠B1BC=90°,D为AC的中点,AB⊥B1D.
如图,在三棱柱ABC-A1B1C1中,AB1=B1B=BA=BC,∠B1BC=90°,D为AC的中点,AB⊥B1D.(Ⅰ)求证:平面ABC⊥平面ABB1A1;
(Ⅱ)求直线B1D与平面ACC1A1所成角的正弦值.
分析 (Ⅰ)取AB中点为O,连接OD,OB1,利用三线合一得到OB1与AB垂直,再由AB与B1D垂直,得到AB垂直于面B1OD,进而得到AB与OD垂直,确定出OD与面ABB1A1垂直,由面ABC过OD,即可得证;
(Ⅱ)由(Ⅰ)知,OB,OD,OB1两两垂直,以O为坐标原点,$\overrightarrow{OB}$的方向为x轴的方向,|$\overrightarrow{OB}$|为单位长度1,建立如图所示的空间直角坐标系O-xyz,表示出B1,D,A,C,C1的坐标,进而确定出$\overrightarrow{{B}_{1}D}$,$\overrightarrow{AC}$,$\overrightarrow{C{C}_{1}}$,设平面ACC1A1的法向量为$\overrightarrow{m}$=(x,y,z),则$\overrightarrow{m}$•$\overrightarrow{AC}$=0,$\overrightarrow{m}$•$\overrightarrow{C{C}_{1}}$=0,取特值法即可确定出直线B1D与平面ACC1A1所成角的正弦值.
解答 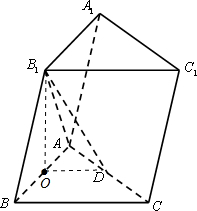 解:(Ⅰ)取AB中点为O,连接OD,OB1,
解:(Ⅰ)取AB中点为O,连接OD,OB1,
∵B1B=B1A,∴OB1⊥AB,
又AB⊥B1D,OB1与B1D交于点B1,
∴AB⊥平面B1OD,
∵OD?平面B1OD,∴AB⊥OD,
由已知,BC⊥BB1,又OD∥BC,
∴OD⊥BB1,
∵AB与BB1交于点B,
∴OD⊥平面ABB1A1,
又OD?平面ABC,
∴平面ABC⊥平面ABB1A1;
(Ⅱ)由(Ⅰ)知,OB,OD,OB1两两垂直,
以O为坐标原点,$\overrightarrow{OB}$的方向为x轴的方向,|$\overrightarrow{OB}$|为单位长度1,建立如图所示的空间直角坐标系O-xyz,
由题设知B1(0,0,$\sqrt{3}$),D(0,1,0),A(-1,0,0),C(1,2,0),C1(0,2,$\sqrt{3}$),
则$\overrightarrow{{B}_{1}D}$=(0,1,-$\sqrt{3}$),$\overrightarrow{AC}$=(2,2,0),$\overrightarrow{C{C}_{1}}$=(-1,0,$\sqrt{3}$),
设平面ACC1A1的法向量为$\overrightarrow{m}$=(x,y,z),则$\overrightarrow{m}$•$\overrightarrow{AC}$=0,$\overrightarrow{m}$•$\overrightarrow{C{C}_{1}}$=0,
即x+y=0,-x+$\sqrt{3}$z=0,
可取$\overrightarrow{m}$=($\sqrt{3}$,-$\sqrt{3}$,1),|cos{$\overrightarrow{{B}_{1}D}$,$\overrightarrow{m}$}|>$\frac{\sqrt{21}}{7}$,
则直线B1D与平面ACC1A1所成角的正弦值是$\frac{\sqrt{21}}{7}$.
点评 此题考查了直线与平面所成的角,平面与平面垂直的判定,做出相应的辅助线是解本题第一问的关键.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案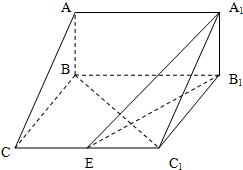 如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,已知AA1=2,AB=$\sqrt{2}$,BC=1,∠BCC1=$\frac{π}{3}$.
如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,已知AA1=2,AB=$\sqrt{2}$,BC=1,∠BCC1=$\frac{π}{3}$.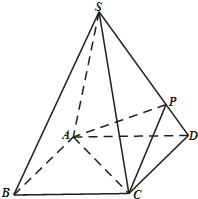 如图,正四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的$\sqrt{2}$倍,点P在侧棱SD上,且SP=3PD.
如图,正四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的$\sqrt{2}$倍,点P在侧棱SD上,且SP=3PD.