题目内容
【题目】已知
为坐标原点，双曲线
上有
两点满足
，且点到直线
的距离为
，则双曲线的离心率为（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】
讨论直线
的斜率是否存在：当斜率不存在时，易得直线的方程，根据
及点O到直线距离即可求得
的关系，进而求得离心率；当斜率存在时，设出直线方程，联立双曲线方程，结合及点到直线距离即可求得离心率。
（1）当直线的斜率不存在时，由点
到直线的距离为
可知直线的方程为
所以线段
因为，根据等腰直角三角形及双曲线对称性可知
，即
双曲线中满足
所以
，化简可得
同时除以
得
，解得
因为
，所以
（2）当直线的斜率存在时，可设直线方程为
，联立方程可得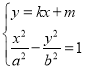
化简可得
设
则
，
因为点到直线的距离为
则
，化简可得
又因为
所以
化简得
即
所以
，双曲线中满足
代入化简可得
求得
，即
因为，所以
综上所述，双曲线的离心率为
所以选A
练习册系列答案
阅读快车系列答案
相关题目
