题目内容
1.已知集合A={x|log2x≤2},B={x|y=log2(a-x)},若A⊆B,求实数a的范围.分析 利用对数函数的单调性求解集合A,对数函数的定义域求解B,通过A⊆B,求实数a的取值范围.
解答 解:集合A={x|log2x≤2}={x|0<x≤4},
B={x|y=log2(a-x)}={x|x<a},
因为A⊆B,所以a>4,
所以实数a的取值范围a>4.
点评 本题考查集合的运算,对数不等式的求法,考查计算能力,比较基础.

练习册系列答案
相关题目
16.函数y=|x+1|+1的图象是( )
| A. | 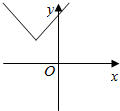 | B. | 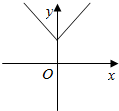 | C. | 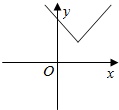 | D. | 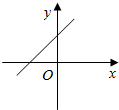 |
 已知函数$f(x)=\left\{\begin{array}{l}-x,-1≤x<0\\{x^2},0≤x<1\\ x,\;1≤x≤2.\end{array}\right.$.
已知函数$f(x)=\left\{\begin{array}{l}-x,-1≤x<0\\{x^2},0≤x<1\\ x,\;1≤x≤2.\end{array}\right.$.