题目内容
在数列{an}中,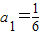 ,
,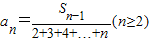 其中Sn表示数列的前n项和.
其中Sn表示数列的前n项和.(Ⅰ)分别求a2,a3,a4的值;
(Ⅱ)求数列{an}的通项公式an的表达式,并予以证明.
【答案】分析:(Ⅰ)通过关系式,利用n=2,3,4,即可求a2,a3,a4的值;
(Ⅱ)通过观察a1,a2,a3,a4的值,猜想求数列{an}的通项公式an的表达式,然后利用数学归纳法证明.
解答:(本小题满分14分)
解:(Ⅰ)因为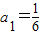 ,
,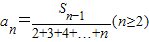 ,
,
所以n=2时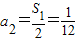 ,
,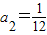 ,
,
n=3时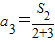 =
=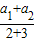 =
= =
=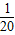 ,
,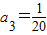 ,
,
n=4时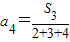 =
=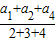 =
=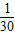 ,
,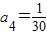 …(3分)
…(3分)
(Ⅱ)由(Ⅰ)猜想数列{an}的通项公式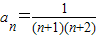 …(5分)
…(5分)
以下用数学归纳法证明:①n=1时,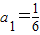 ,命题成立;
,命题成立;
②假设n=k(k≥1)时成立,即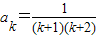 成立…(7分)
成立…(7分)
由已知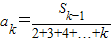
推得: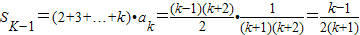
成立…(9分)
那么,当n=k+1时,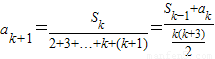 =
=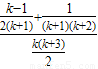
=
则n=k+1时,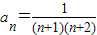 也成立.…(14分)
也成立.…(14分)
综上可知,对任意n∈N,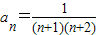 成立.
成立.
点评:本题是中档题,考查数列的递推关系式的应用,数列的项的求法,数学归纳法的证明方法,注意证明中必须利用假设,考查计算能力,逻辑推理能力.
(Ⅱ)通过观察a1,a2,a3,a4的值,猜想求数列{an}的通项公式an的表达式,然后利用数学归纳法证明.
解答:(本小题满分14分)
解:(Ⅰ)因为
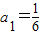 ,
,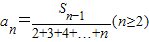 ,
,所以n=2时
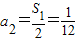 ,
,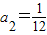 ,
,n=3时
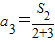 =
=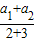 =
= =
=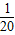 ,
,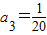 ,
,n=4时
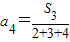 =
=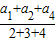 =
=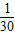 ,
,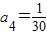 …(3分)
…(3分)(Ⅱ)由(Ⅰ)猜想数列{an}的通项公式
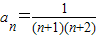 …(5分)
…(5分)以下用数学归纳法证明:①n=1时,
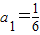 ,命题成立;
,命题成立;②假设n=k(k≥1)时成立,即
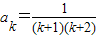 成立…(7分)
成立…(7分)由已知
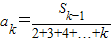
推得:
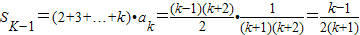
成立…(9分)
那么,当n=k+1时,
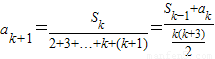 =
=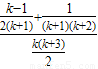
=

则n=k+1时,
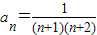 也成立.…(14分)
也成立.…(14分)综上可知,对任意n∈N,
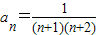 成立.
成立.点评:本题是中档题,考查数列的递推关系式的应用,数列的项的求法,数学归纳法的证明方法,注意证明中必须利用假设,考查计算能力,逻辑推理能力.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目