题目内容
(本题满分14分)
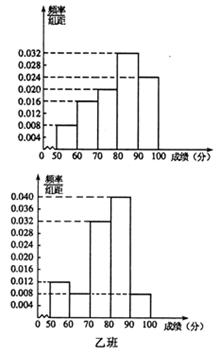
有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表.
已知在全部105人中抽到随机抽取1人为优秀的概率为
(1)请完成上面的列联表;
(2)根据列联表的数据,若按 的可靠性要求,能否认为“成绩与班级有关系” .
的可靠性要求,能否认为“成绩与班级有关系” .
(3)若按下面的方法从甲班优秀的学生抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到6或10号的概率.
有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表.
| | 优秀 | 非优秀 | 总计 |
| 甲班 | 10 | | |
| 乙班 | | 30 | |
| 合计 | | | 105 |

(1)请完成上面的列联表;
(2)根据列联表的数据,若按
 的可靠性要求,能否认为“成绩与班级有关系” .
的可靠性要求,能否认为“成绩与班级有关系” .(3)若按下面的方法从甲班优秀的学生抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到6或10号的概率.
(Ⅰ)表格如下
(Ⅱ)有95%的把握认为“成绩与班级有关系”.
(Ⅲ)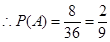 。
。
| | 优秀 | 非优秀 | 总计 |
| 甲班 | 10 | 45 | 55 |
| 乙班 | 20 | 30 | 50 |
| 合计 | 30 | 75 | 105 |
(Ⅱ)有95%的把握认为“成绩与班级有关系”.
(Ⅲ)
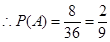 。
。(1)根据优秀的人数为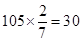 ,非优秀人数为75,可以填完整列联表.
,非优秀人数为75,可以填完整列联表.
(II)根据列联表求出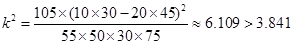 ,从而确定有95%的把握认为“成绩与班级有关系”.
,从而确定有95%的把握认为“成绩与班级有关系”.
(III) 设“抽到6或10号”为事件A,先后两次抛掷一枚均匀的骰子,出现的点数为(x,y),计算出总的基本事件的个数为36个.再根据事件A包含的基本事件有8个.再根据古典概型概率计算公式计算即可.
(Ⅰ)表格如下
(Ⅱ):根据列联表中的数据,得到
 …………………5分
…………………5分
因此有95%的把握认为“成绩与班级有关系”. ………………7分
(Ⅲ)设“抽到6或10号”为事件A,先后两次抛掷一枚均匀的骰子,出现的点数为(x,y)…………………8分
所有的基本事件有(1,1)、(1,2)、(1,3)、…、(6,6),共36个.……………10分
事件A包含的基本事件有:
(1,5)、(2,4)、(3,3)、(4,2)、(5,1)(4,6)、(5,5)、(6、4),共8个……12分
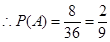 …………………14分
…………………14分
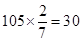 ,非优秀人数为75,可以填完整列联表.
,非优秀人数为75,可以填完整列联表.(II)根据列联表求出
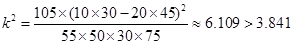 ,从而确定有95%的把握认为“成绩与班级有关系”.
,从而确定有95%的把握认为“成绩与班级有关系”.(III) 设“抽到6或10号”为事件A,先后两次抛掷一枚均匀的骰子,出现的点数为(x,y),计算出总的基本事件的个数为36个.再根据事件A包含的基本事件有8个.再根据古典概型概率计算公式计算即可.
(Ⅰ)表格如下
| | 优秀 | 非优秀 | 总计 |
| 甲班 | 10 | 45 | 55 |
| 乙班 | 20 | 30 | 50 |
| 合计 | 30 | 75 | 105 |
(Ⅱ):根据列联表中的数据,得到
 …………………5分
…………………5分因此有95%的把握认为“成绩与班级有关系”. ………………7分
(Ⅲ)设“抽到6或10号”为事件A,先后两次抛掷一枚均匀的骰子,出现的点数为(x,y)…………………8分
所有的基本事件有(1,1)、(1,2)、(1,3)、…、(6,6),共36个.……………10分
事件A包含的基本事件有:
(1,5)、(2,4)、(3,3)、(4,2)、(5,1)(4,6)、(5,5)、(6、4),共8个……12分
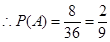 …………………14分
…………………14分
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目

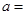



 ,求随机变量
,求随机变量

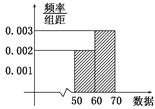
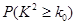
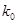
 ,求
,求 列联表,并判断是否有
列联表,并判断是否有 的把握认为:“成绩优秀”与教学方式有关.
的把握认为:“成绩优秀”与教学方式有关.


 的样本,样本中A型号产品有15件,那么样本容量
的样本,样本中A型号产品有15件,那么样本容量