题目内容
为适应新课改,切实减轻学生负担,提高学生综合素质,某市某学校高三年级文科生300人在数学选修4-4、4-5、4-7选课方面进行改革,由学生自由选择2门(不可多选或少选),选课情况如下表:
(1)为了解学生情况,现采用分层抽样方法抽取了三科作业共50本,统计发现4-5有18本,试根据这一数据求出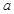 ,
, 的值.
的值.
(2)为方便开课,学校要求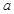 ≥110,
≥110, >110,计算
>110,计算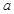 >
> 的概率.
的概率.
| | 4-4 | 4-5 | 4-7 |
| 男生 | 130 | 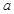 | 80 |
| 女生 |  | 100 | 60 |
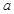 ,
, 的值.
的值.(2)为方便开课,学校要求
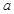 ≥110,
≥110, >110,计算
>110,计算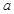 >
> 的概率.
的概率.(1)a="116" b=114(2)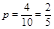
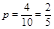
(1)由每生选2科知共有600人次选课,所以按分层抽样得: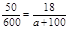 ,所以a=116,从而b="114" 5分
,所以a=116,从而b="114" 5分
(2)因为a+b=230,a≥110,b>110,所以(a,b)的取值有:(110,120)(111,119)(112,118)(113,117)(114,116)(115,115)(116,114)(117,113)(118,112)(119,111)共10种;·········· 8分
其中a>b的情况有(116,114)(117,113)(118,112)(119,111)共4种;···· 10分
所以a>b的概率为: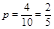 ························ 12分
························ 12分
(1)根据分层抽样的规则,各层在样本中的占比与其在总体中的占比相等建立关于a、b的方程,
(2)因为a+b=200,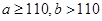 ,列出满足此条件的取值(a,b).然后再从中找到a>b的(a,b),再根据古典概型概率计算公式计算即可.
,列出满足此条件的取值(a,b).然后再从中找到a>b的(a,b),再根据古典概型概率计算公式计算即可.
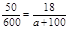 ,所以a=116,从而b="114" 5分
,所以a=116,从而b="114" 5分(2)因为a+b=230,a≥110,b>110,所以(a,b)的取值有:(110,120)(111,119)(112,118)(113,117)(114,116)(115,115)(116,114)(117,113)(118,112)(119,111)共10种;·········· 8分
其中a>b的情况有(116,114)(117,113)(118,112)(119,111)共4种;···· 10分
所以a>b的概率为:
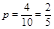 ························ 12分
························ 12分(1)根据分层抽样的规则,各层在样本中的占比与其在总体中的占比相等建立关于a、b的方程,
(2)因为a+b=200,
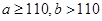 ,列出满足此条件的取值(a,b).然后再从中找到a>b的(a,b),再根据古典概型概率计算公式计算即可.
,列出满足此条件的取值(a,b).然后再从中找到a>b的(a,b),再根据古典概型概率计算公式计算即可.
练习册系列答案
相关题目


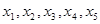 的平均数是2,方差是
的平均数是2,方差是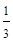 ,那么另一组数据
,那么另一组数据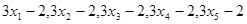 的平均数和方差分别为( )
的平均数和方差分别为( )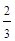

 的可靠性要求,能否认为“成绩与班级有关系” .
的可靠性要求,能否认为“成绩与班级有关系” .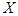 表示一位申请者经过考试的次数,据统计数据分析知
表示一位申请者经过考试的次数,据统计数据分析知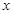
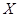 次考试需缴纳费用
次考试需缴纳费用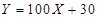 (单位:元),求两位申请者所需费用的和小于500元的概率;
(单位:元),求两位申请者所需费用的和小于500元的概率;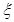 ,求
,求 如下,其中拟合效果最好的模型是________.
如下,其中拟合效果最好的模型是________.