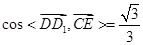题目内容
本小题满分14分)
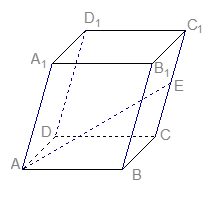
如图,在直三棱柱 中,
中, ,
, ,
, ,点
,点 、
、 分别是
分别是 、
、 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)证明:平面 平面
平面 ;
;
(Ⅲ)求多面体A1B1C1BD的体积V.
(Ⅰ)证明:见解析(Ⅱ)证明:见解析;
(Ⅲ)V=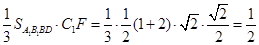 。
。
解析试题分析:(I)根据线面平行的判定定理只需证明:AE//平面BC1D即可.
(II)因为 ,所以
,所以 ,然后再利用勾股定理证明
,然后再利用勾股定理证明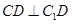 ,
,
从而可证明: ,再根据面面垂直的判定定理得平面
,再根据面面垂直的判定定理得平面 平面
平面 .
.
(III) 取A1B1中点F,易证:C1F⊥面A1B1BD,从而得到所求四棱锥 的高,然后再根据棱锥的体积计算公式计算即可.
的高,然后再根据棱锥的体积计算公式计算即可.
(Ⅰ)证明:在矩形 中,
中,
由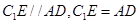
得 是平行四边形.…………………1分
是平行四边形.…………………1分
所以 , …………………2分
, …………………2分
又 平面
平面 ,
, 平面
平面 ,
,
所以 平面
平面 …………………4分
…………………4分
(Ⅱ)证明:直三棱柱 中,
中,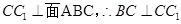 ,
, ,
,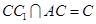 ,所以
,所以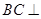 平面
平面 ,…………………6分
,…………………6分
而 平面
平面 ,所以
,所以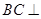
 .…………………7分
.…………………7分
在矩形 中,
中, ,从而
,从而 ,
,
所以
 , …………………8分
, …………………8分
又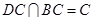 ,所以
,所以 平面
平面 , …………………9分
, …………………9分
而 平面
平面 ,所以平面
,所以平面 平面
平面 …………………10分
…………………10分
(Ⅲ)取A1B1中点F,由A1C1=B1C1知C1F⊥A1B1,……………11分
又直三棱柱中侧面ABA1B1⊥底面A1B1C1且交线为A1B1,故C1F⊥面A1B1BD,……12分
∴V=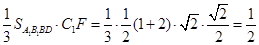 …………………14分
…………………14分
考点:线线,线面,面面平行与垂直的判定与性质,棱锥的体积.
点评:掌握线线、线面,面面垂直的判定与性质定理是解决此类证明的关键,并且还要记住柱,锥,台体的体积及表面积公式.

练习册系列答案
相关题目
 点
点 上,过点
上,过点 做
做 //
// 将
将 的位置(
的位置( ),
), .
.
 (II)试问:当点
(II)试问:当点 的平面角的余弦值是否为定值?若是,求出定值,若不是,说明理由.
的平面角的余弦值是否为定值?若是,求出定值,若不是,说明理由. 中,
中,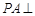 平面
平面 ,
,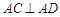 ,
,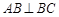 ,
,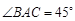 ,
,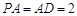 ,
,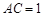 .
.
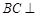 平面
平面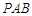
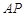 和平面
和平面 所成角的正弦值
所成角的正弦值 的正切值;
的正切值;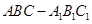 中,
中, ,
,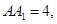 点
点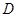 是
是 的中点。
的中点。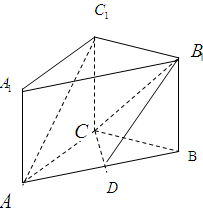

 与平面
与平面 所成的角的正切值
所成的角的正切值 与直角梯形
与直角梯形 垂直,
垂直, ,
, ,
, ,
, .若
.若 分别为
分别为 的中点.(1)求
的中点.(1)求 的值; (2)求面
的值; (2)求面 与面
与面 所成的二面角大小.
所成的二面角大小.
 中,
中, 底面
底面 ,四边形
,四边形 ,
, ,
,  ,
, ,E为
,E为 中点.
中点.
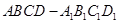 中,
中,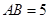 ,
,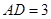 ,
,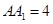 ,
,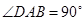 ,
,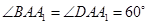 ,
, 是
是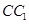 的中点,设
的中点,设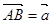 ,
,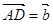 ,
, .
.
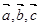 表示
表示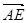 ;
; 的长.
的长.