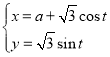题目内容
【题目】已知动点P是△PMN的顶点,M(﹣2,0),N(2,0),直线PM,PN的斜率之积为﹣![]() .
.
(1)求点P的轨迹E的方程;
(2)设四边形ABCD的顶点都在曲线E上,且AB∥CD,直线AB,CD分别过点(﹣1,0),(1,0),求四边形ABCD的面积为![]() 时,直线AB的方程.
时,直线AB的方程.
【答案】(1)![]() (x≠±2);(2)x±y+1=0.
(x≠±2);(2)x±y+1=0.
【解析】
(1)设点P(x,y),直接把已知条件用坐标表示并化简即可;
(2)设直线AB的方程为x=my﹣1,A(x1,y1),B(x2,y2),由直线与椭圆相交弦长公式(应用韦达定理计算)求出弦长,交求出原点到直线![]() 距离,表示出
距离,表示出![]() 面积,由对称性知四边形ABCD的面积是
面积,由对称性知四边形ABCD的面积是![]() 面积的4倍,从而可以求出
面积的4倍,从而可以求出![]() .
.
解:(1)设点P(x,y),
∵直线PM与PN的斜率之积为﹣![]() ,
,
即![]() =
=![]() =﹣
=﹣![]() ,
,
化简得![]() (x≠±2),
(x≠±2),
∴动点P的轨迹E的方程为![]() (x≠±2);
(x≠±2);
(2)设直线AB的方程为x=my﹣1,A(x1,y1),B(x2,y2),
由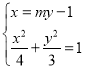
得(3m2+4)y2﹣6my﹣9=0,
则 ![]() , y1+y2=
, y1+y2=![]() ,
,![]() ,
,
|y1﹣y2|=![]() =
=![]() ,
,
∴|AB|=![]() =
=![]() ,
,
又原点O到直线AB的距离d=![]() ,
,
∴S△ABO=![]() ×
×![]() =
=![]() ,
,
由图形的对称性可知,SABCD=4S△ABO,
∴SABCD=![]() =
=![]() ,
,
化简得18m4﹣m2﹣17=0,
解得m2=1,即m=±1,
∴直线AB的方程为x=±y﹣1,即x±y+1=0.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案【题目】空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如下表:
AQI指数值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
下图是某市10月1日—20日AQI指数变化趋势:

下列叙述错误的是
A. 这20天中AQI指数值的中位数略高于100
B. 这20天中的中度污染及以上的天数占![]()
C. 该市10月的前半个月的空气质量越来越好
D. 总体来说,该市10月上旬的空气质量比中旬的空气质量好