题目内容
15.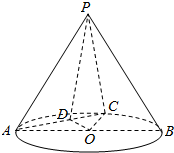 如图,在圆锥PO中,已知PO=$\sqrt{2}$,圆O的直径AB=2,C是弧AB的中点,D为AC的中点.
如图,在圆锥PO中,已知PO=$\sqrt{2}$,圆O的直径AB=2,C是弧AB的中点,D为AC的中点.(1)求异面直线PD和BC所成的角
(2)求直线OC和平面PAC所成角的正弦值.
分析 (1)由已知得OD∥BC,从而异面直线PD和BC所成的角为∠PDO,由此能求出异面直线PD和BC所成的角.
(2)在平面POD中,过O作OH⊥PD于H,由已知得∠OCH是直线OC和平面PAC所成的角.由此能求出直线OC和平面PAC所成角的正弦值.
解答 解:(1)∵O,D分别是AB和AC的中点,∴OD∥BC,
∴异面直线PD和BC所成的角为∠PDO,
在△ABC中,AB=2,C是AB的中点,D为AC的中点,
∴$AC=BC=\sqrt{2}\;,OD=\frac{{\sqrt{2}}}{2}$,
又∵$PO=\sqrt{2}$,PO⊥面ABC,
∴$tan∠PDO=\frac{PO}{OD}=2$,
∴异面直线PD和BC所成的角为arctan2.
(2)∵OA=OC,D是AC的中点,∴AC⊥OD,
又PO⊥底面ABC,AC?底面ABC,∴AC⊥PO,
∵OD∩PO=O,∴AC⊥平面POD,
又AC?平面PAC,∴平面POD⊥平面PAC,
在平面POD中,过O作OH⊥PD于H,
则OH⊥平面PAC,连结CH,则CH是OC在平面PAC上的射影,
∴∠OCH是直线OC和平面PAC所成的角.
在Rt△POD中,OH=$\frac{PO•OD}{\sqrt{P{O}^{2}+O{D}^{2}}}$=$\frac{\sqrt{2}×\frac{1}{2}}{\sqrt{2+\frac{1}{4}}}$=$\frac{\sqrt{2}}{3}$,
在Rt△OHC中,sin∠OCH=$\frac{OH}{OC}$=$\frac{\sqrt{2}}{3}$.
∴直线OC和平面PAC所成角的正弦值为$\frac{\sqrt{2}}{3}$.
点评 本题考查异面直线所成角的大小的求法,考查线面解的正弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

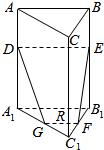 如图,在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,D、E分别在AA1、BB1上,AD=BE=1,F、G分别是B1C1、A1C1的中点,则直线GF与直线DE的距离为( )
如图,在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,D、E分别在AA1、BB1上,AD=BE=1,F、G分别是B1C1、A1C1的中点,则直线GF与直线DE的距离为( )| A. | $\sqrt{3}$ | B. | $\frac{3\sqrt{6}}{4}$ | C. | $\frac{2\sqrt{5}}{3}$ | D. | $\frac{\sqrt{19}}{2}$ |
| A. | $\frac{2\sqrt{34}}{17}$ | B. | $\frac{3\sqrt{17}}{17}$ | C. | -$\frac{2\sqrt{34}}{17}$ | D. | -$\frac{3\sqrt{17}}{17}$ |
 如图:在三棱柱ABC-A1B1C1中,四边形A1ABB1是菱形,四边形BCC1B1是矩形,且C1B1⊥AB.
如图:在三棱柱ABC-A1B1C1中,四边形A1ABB1是菱形,四边形BCC1B1是矩形,且C1B1⊥AB.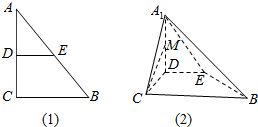 如图(1),在Rt△ABC中,∠C=90°,BC=2,AC=4,点D,E分别是AC,AB的中点,将△ADE沿DE折起到△A1DE的位置,使A1D⊥DC如图(2)所示,M为A1D的中点,求CM与面A1EB所成角的正弦值.
如图(1),在Rt△ABC中,∠C=90°,BC=2,AC=4,点D,E分别是AC,AB的中点,将△ADE沿DE折起到△A1DE的位置,使A1D⊥DC如图(2)所示,M为A1D的中点,求CM与面A1EB所成角的正弦值.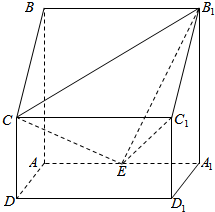 四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥CD,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.
四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥CD,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.