题目内容
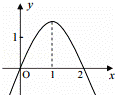
己知函数f（x）=ax3+bx2+c，其导数f'（x）的图象如图所示，则函数f（x）的极大值是（ ）
|
| A． | a+b+c | B． | 8a+4b+c | C． | 3a+2b | D． | c |
考点：
利用导数研究函数的极值．
专题：
数形结合．
分析：
利用导函数图象，由导函数的图象求出函数的单调区间，求出函数的极值即可．
解答：
解：由导函数的图象知，
f（x）在（1，2）递增；在（2，+∞）上递减
所以当x=2时取得极大值，
极大值为：f（2）=8a+4b+c
则函数f（x）的极大值是8a+4b+c
故选B．
点评：
本题主要考查了利用导数研究函数的极值，求函数的极值问题，通常利用导数求出函数的极值．
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
己知函数f（x）=3cos（2x-
）（x∈R），则下列结论错误的是（ ）
| π |
| 3 |
A、函数f（x）的图象的一条对称轴为x=
| ||||
B、点（-
| ||||
C、函数f（x）在区间（
| ||||
D、函数f（x）的图象可以由函数g（x）=3cos2x图象向右平移
|
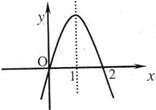
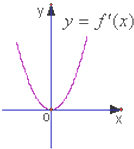己知函数f（x）是定义域为R的奇函数，且f（-5）=-1，f（x）的导函数y=f′（x）的图象如图所示．若正数a满足f（2a+1）＜1，则