题目内容
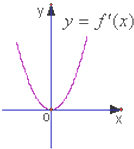 己知函数f(x)是定义域为R的奇函数,且f(-5)=-1,f(x)的导函数y=f′(x)的图象如图所示.若正数a满足f(2a+1)<1,则-
己知函数f(x)是定义域为R的奇函数,且f(-5)=-1,f(x)的导函数y=f′(x)的图象如图所示.若正数a满足f(2a+1)<1,则-| 1 |
| a |
分析:由函数的导函数的图象判断出导函数的符号,从而得到原函数的单调性,再由f(-5)=-1,得f(5)=1,
代入f(2a+1)<1后由单调性得到不等式2a+1<5,求出a的范围后可求答案.
代入f(2a+1)<1后由单调性得到不等式2a+1<5,求出a的范围后可求答案.
解答:解:由f(x)的导函数y=f′(x)的图象可知,
当x∈(-∞,+∞)时,f′(x)≥0恒成立,
所以函数f(x)在(-∞,+∞)上为增函数,
因为函数f(x)是定义域为R的奇函数,
由f(-5)=-1,得f(5)=1.
则由f(2a+1)<1,得f(2a+1)<f(5),
所以2a+1<5,解得a<2.
又a>0,所以
>
.
则-
<-
.
故选B.
当x∈(-∞,+∞)时,f′(x)≥0恒成立,
所以函数f(x)在(-∞,+∞)上为增函数,
因为函数f(x)是定义域为R的奇函数,
由f(-5)=-1,得f(5)=1.
则由f(2a+1)<1,得f(2a+1)<f(5),
所以2a+1<5,解得a<2.
又a>0,所以
| 1 |
| a |
| 1 |
| 2 |
则-
| 1 |
| a |
| 1 |
| 2 |
故选B.
点评:本题主要考查函数的单调性与其导函数的正负之间的关系,考查了函数的奇偶性,练习了不等式的解法,是中档题.

练习册系列答案
相关题目
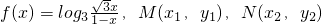 是f(x)图象点的两点,横坐标为
是f(x)图象点的两点,横坐标为 的点P是M,N的中点.
的点P是M,N的中点.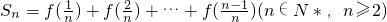 ,
,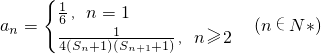 ,Tn为数列{an}前n项和,当Tn<m(Sn+1+1)对一切n∈N*都成立时,试求实数m的取值范围.
,Tn为数列{an}前n项和,当Tn<m(Sn+1+1)对一切n∈N*都成立时,试求实数m的取值范围.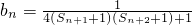 ,Bn为数列{bn}前n项和,证明:
,Bn为数列{bn}前n项和,证明: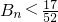 .
.