题目内容
8.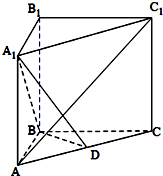 如图所示,在三棱柱ABC-A1B1C1中,BB1⊥底面A1B1C1,A1B1⊥B1C1且A1B1=BB1=B1C1,D为AC的中点.
如图所示,在三棱柱ABC-A1B1C1中,BB1⊥底面A1B1C1,A1B1⊥B1C1且A1B1=BB1=B1C1,D为AC的中点.(Ⅰ)求证:A1B⊥AC1
(Ⅱ)在直线CC1上是否存在一点E,使得A1E⊥平面A1BD,若存在,试确定E点的位置;若不存在,请说明理由.
分析 (Ⅰ)连接AB1,利用三棱柱的性质容易得到B1C1⊥BB1,结合已知,根据线面垂直的判定定理得到B1C1⊥平面A1B1BA,进一步由线面垂直的判定定理和性质定理得到所证;
(Ⅱ)存在点E在CC1的延长线上且CE=2CC1时,A1E⊥平面A1BD.利用线面垂直的判定定理和性质定理矩形证明.
解答 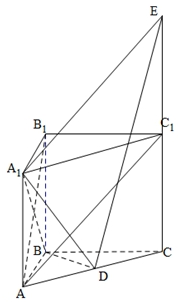 (Ⅰ)证明:连接AB1
(Ⅰ)证明:连接AB1
∵BB1⊥平面A1B1C1
∴B1C1⊥BB1
∵B1C1⊥A1B1且A1B1∩BB1=B1
∴B1C1⊥平面A1B1BA
∴A1B⊥B1C1 …(3分)
又∵A1B⊥AB1且AB1∩B1C1=B1
∴A1B⊥平面AB1C1 …(5分)
∴A1B⊥AC1 …(6分)
(Ⅱ)存在点E在CC1的延长线上且CE=2CC1时,A1E⊥平面A1BD.…(7分)
设AB=a,CE=2a,∴${A}_{1}{C}_{1}=\sqrt{2}a$,
∴${A}_{1}E=\sqrt{3}a$,${A}_{1}D=\sqrt{\frac{3}{2}}a$,DE=$\sqrt{\frac{9}{2}}a$,
∴${A}_{1}{E}^{2}+{A}_{1}{D}^{2}=D{E}^{2}$,∴A1E⊥A1D…(9分)
∵BD⊥AC,BD⊥CC1,AC∩CC1=C
∴BD⊥平面ACC1A1 …(10分)
又A1E?平面ACC1A1
∴A1E⊥BD
又BD∩A1D=D
∴A1E⊥平面A1BD …(12分)
点评 本题邑三棱柱为载体,考查了空间线面垂直的判定定理和性质定理的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下面几种推理中是演绎推理的序号为( )
| A. | 半径为r圆的面积S=πr2,则单位圆的面积S=π | |
| B. | 由金、银、铜、铁可导电,猜想:金属都可导电 | |
| C. | 由平面三角形的性质,推测空间四面体性质 | |
| D. | 由平面直角坐标系中圆的方程为(x-a)2+(y-b)2=r2,推测空间直角坐标系中球的方程为(x-a)2+(y-b)2+(z-c)2=r |
16.已知不等式①${2^{{x^2}-4x+3}}<1$,②$\frac{2}{4-x}≥1$,③2x2-9x+m<0,要使同时满足①和②的所有x都满足③,则实数m的取值范围是( )
| A. | m<9 | B. | m≤9 | C. | m<10 | D. | m≤10 |
3.已知x、y的取值如表所示:
从散点图分析,y与x线性相关,且$\hat y$=0.95x+a,则a=2.6.
| x | 0 | 1 | 3 | 4 |
| y | 2.2 | 4.3 | 4.8 | 6.7 |