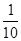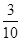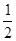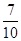题目内容
甲、乙两个盒子中各有3个球,其中甲盒中有2个黑球1个白球,乙盒中有1个黑球2个白球,所有球之间只有颜色区别.
(Ⅰ)若从甲、乙两个盒子中各取一个球,求取出的2个球颜色相同的概率;
(Ⅱ)将这两个盒子中的球混合在一起,从中任取2个, 求取出的2个球中至少有一个黑球的概率.
(Ⅰ)若从甲、乙两个盒子中各取一个球,求取出的2个球颜色相同的概率;
(Ⅱ)将这两个盒子中的球混合在一起,从中任取2个, 求取出的2个球中至少有一个黑球的概率.
(1)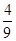 ;(2)
;(2)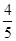
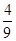 ;(2)
;(2)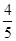
试题分析:(Ⅰ)列出所有可能结果计算符合条件的结果数. (Ⅱ)列出所有基本事件可能结果,计算符合条件的事件结果数.
试题解析:将甲盒中的2个黑球1个白球分别记为
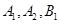 ;
;乙盒子中的1个黑球2个白球分别记为
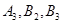 . 1分
. 1分(Ⅰ)“从甲、乙两个盒子中各取一个球”的基本事件有:
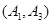
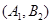
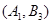
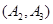
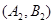
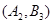
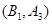
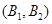
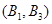 ,共9个. 3分
,共9个. 3分记取出的2个球颜色相同为事件M,则事件M包含的基本事件有:
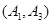
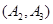
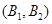
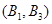 ,共4个. 5分
,共4个. 5分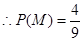 . 6分
. 6分(Ⅱ)“从6个球中任取两个球”的基本事件有:
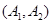
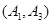
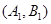
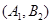
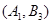
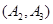
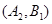
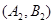
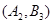
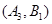
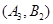
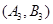
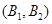
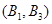
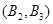 ,
,共15个. 8分
设“取出的2个球中至少有一个黑球”为事件N,则事件N包含的基本事件有:
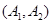
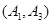
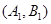
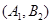
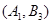
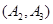
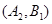
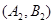
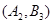
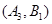
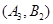
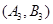 共12个. 10分
共12个. 10分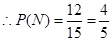 . 12分
. 12分(也可用间接法)

练习册系列答案
相关题目
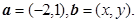
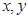 分别表示将一枚质地均匀的骰子先后抛掷两次时第一次、第二次正面朝上出现的点数,求满足
分别表示将一枚质地均匀的骰子先后抛掷两次时第一次、第二次正面朝上出现的点数,求满足 的概率.
的概率.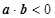 的概率.
的概率.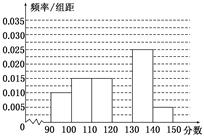
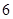 个面的中心,甲从这
个面的中心,甲从这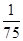
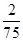
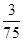
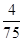
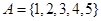 中任取三个元素构成三元有序数组
中任取三个元素构成三元有序数组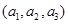 ,规定
,规定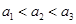
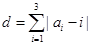 ,(其中
,(其中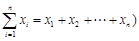 ,从所有三元有序数组中任选一个,求它的“项标距离”
,从所有三元有序数组中任选一个,求它的“项标距离”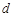 为偶数的概率;
为偶数的概率;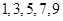 ,从这
,从这 条线段中任取
条线段中任取 条,则所取
条,则所取