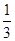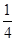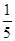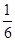题目内容
将一颗骰子先后抛掷2次,观察向上的点数,求:
(Ⅰ)两数之和为5的概率;
(Ⅱ)两数中至少有一个为奇数的概率.
(Ⅰ)两数之和为5的概率;
(Ⅱ)两数中至少有一个为奇数的概率.
(Ⅰ)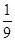 ;(Ⅱ)
;(Ⅱ)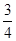 .
.
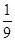 ;(Ⅱ)
;(Ⅱ)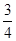 .
.试题分析:(Ⅰ)通过列举可发现此问题中含有36个基本事件,而两数之和为5的有(1,4)、(4,1)、(2.3)、(3、2)4种,利用古典概型概率计算公式可得概率为
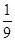 ;(Ⅱ)求出对立面的概率:对立面含的基本事件为(2,2)、(4,4)、(6,6)、(2,4)、(4,2)、(2,6)、(6,2)、(4,6)、(6、4)共9种,所以所求的概率为
;(Ⅱ)求出对立面的概率:对立面含的基本事件为(2,2)、(4,4)、(6,6)、(2,4)、(4,2)、(2,6)、(6,2)、(4,6)、(6、4)共9种,所以所求的概率为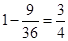 .
.试题解析:将一颗骰子先后抛掷2次,此问题中含有36个等可能基本事件.
(Ⅰ)记“两数之和为5”为事件A,则事件A中含有4个基本事件,所以
P(A)=
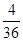 =
=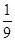 .
.答:两数之和为5的概率为
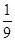 . 6分
. 6分(Ⅱ)记“两数中至少有一个为奇数”为事件B,则事件B与“两数均为偶数”为对立事件,所以P(B)=1-
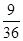 =
=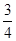 .
.答:两数中至少有一个为奇数的概率为
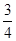 . 12分
. 12分
练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
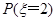 ;
;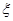 的分布列和数学期望.
的分布列和数学期望.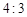 .假设从袋中任取
.假设从袋中任取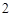 个球,取到的都是红球的概率为
个球,取到的都是红球的概率为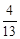 .那么袋中的红球有 __个.
.那么袋中的红球有 __个.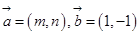 的夹角为
的夹角为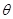 ,则
,则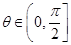 的概率是( )
的概率是( )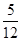
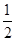
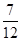
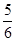
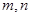 作为点
作为点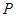 的横、纵坐标,则点
的横、纵坐标,则点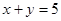 上的概率为 .
上的概率为 .