题目内容
从集合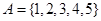 中任取三个元素构成三元有序数组
中任取三个元素构成三元有序数组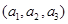 ,规定
,规定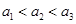
(1)从所有三元有序数组中任选一个,求它的所有元素之和等于10的概率;
(2)定义三元有序数组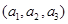 的“项标距离”为
的“项标距离”为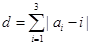 ,(其中
,(其中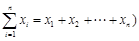 ,从所有三元有序数组中任选一个,求它的“项标距离”
,从所有三元有序数组中任选一个,求它的“项标距离”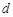 为偶数的概率;
为偶数的概率;
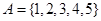 中任取三个元素构成三元有序数组
中任取三个元素构成三元有序数组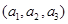 ,规定
,规定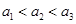
(1)从所有三元有序数组中任选一个,求它的所有元素之和等于10的概率;
(2)定义三元有序数组
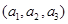 的“项标距离”为
的“项标距离”为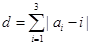 ,(其中
,(其中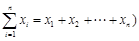 ,从所有三元有序数组中任选一个,求它的“项标距离”
,从所有三元有序数组中任选一个,求它的“项标距离”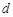 为偶数的概率;
为偶数的概率;(1)0.2 (2)0.6
试题分析:(1)从集合
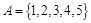 中任取三个不同元素构成三元有序数组如下
中任取三个不同元素构成三元有序数组如下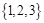

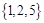
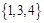
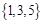
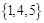
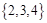
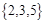
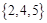
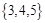
所有元素之和等于10的三元有序数组有
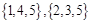
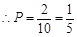
(2)项标距离为0的三元有序数组:
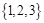
项标距离为2的三元有序数组:
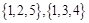
项标距离为4的三元有序数组:
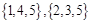
项标距离为6的三元有序数组:
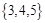
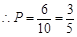
点评:主要是考查了古典概型概率的求解,利用等可能事件的概率求解即可,属于基础题。

练习册系列答案
相关题目
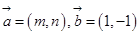 的夹角为
的夹角为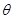 ,则
,则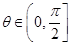 的概率是( )
的概率是( )
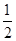
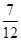
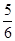
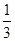
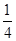

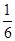
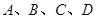 四个不同岗位服务,每个岗位至少有一名志愿者,则甲、乙两人同时参加岗位
四个不同岗位服务,每个岗位至少有一名志愿者,则甲、乙两人同时参加岗位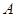 服务的概率是 .
服务的概率是 .