题目内容
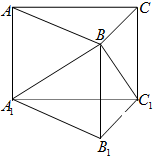 如图,直三棱柱ABC-A1B1C1侧面AA1B1B是边长为5的正方形,AB⊥BC,AC与BC1成60°角,则AC长( )
如图,直三棱柱ABC-A1B1C1侧面AA1B1B是边长为5的正方形,AB⊥BC,AC与BC1成60°角,则AC长( )分析:设BC=a,连接BA1,BC1,根据AC与BC1成60°角可得∠A1C1B=60°,根据直三棱柱ABC-A1B1C1的侧面AA1B1B是边长为5的正方形可得出△BA1C1为等边三角形,故BA1=BC1,可求出a,再借助AB⊥BC,即可求出AC长.
解答: 解:设BC=a,连接BA1,BC1
解:设BC=a,连接BA1,BC1
∵三棱柱ABC-A1B1C1是直三棱柱且侧面AA1B1B是边长为5的正方形
∴AB=CC1=5
∴根据勾股定理可得A1B2=50,
∵AB⊥BC
∴AC2=25+a2
∵在△C1B1B中,BC12=25+a2
∴BC1=AC
∴△BA1C1为等腰三角形
∵AC与BC1成60°角且AC∥A1C1
∴∠A1C1B=60°
∴△BA1C1为等边三角形
∴50=25+a2
∴a=5
∴AC=5
故选D.
 解:设BC=a,连接BA1,BC1
解:设BC=a,连接BA1,BC1∵三棱柱ABC-A1B1C1是直三棱柱且侧面AA1B1B是边长为5的正方形
∴AB=CC1=5
∴根据勾股定理可得A1B2=50,
∵AB⊥BC
∴AC2=25+a2
∵在△C1B1B中,BC12=25+a2
∴BC1=AC
∴△BA1C1为等腰三角形
∵AC与BC1成60°角且AC∥A1C1
∴∠A1C1B=60°
∴△BA1C1为等边三角形
∴50=25+a2
∴a=5
∴AC=5
| 2 |
故选D.
点评:本题主要考查了空间中距离的计算,考查学生的计算能力,属于中档题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 如图,直三棱柱ABC-A1B1C1中,
如图,直三棱柱ABC-A1B1C1中, 如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点.
如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点. 如图在直三棱柱ABC-A1B1C1中∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是
如图在直三棱柱ABC-A1B1C1中∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点. 如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.
如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.