题目内容
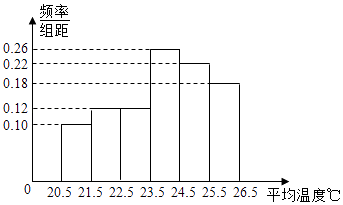
【题目】某市居民用水拟实行阶梯水价,每人月用水量中不超过w立方米的部分按4元/立方米收费,超出w立方米的部分按10元/立方米收费,从该市随机调查了10000位居民,获得了他们某月的用水量数据,整理得到如图频率分布直方图: 
(1)如果w为整数,那么根据此次调查,为使80%以上居民在该月的用水价格为4元/立方米,w至少定为多少?
(2)假设同组中的每个数据用该组区间的右端点值代替,当w=3时,估计该市居民该月的人均水费.
【答案】
(1)解:由频率分布直方图得:
用水量在[0.5,1)的频率为0.1,
用水量在[1,1.5)的频率为0.15,
用水量在[1.5,2)的频率为0.2,
用水量在[2,2.5)的频率为0.25,
用水量在[2.5,3)的频率为0.15,
用水量在[3,3.5)的频率为0.05,
用水量在[3.5,4)的频率为0.05,
用水量在[4,4.5)的频率为0.05,
∵用水量小于等于3立方米的频率为85%,
∴为使80%以上居民在该用的用水价为4元/立方米,
∴w至少定为3立方米
(2)解:当w=3时,该市居民的人均水费为:
(0.1×1+0.15×1.5+0.2×2+0.25×2.5+0.15×3)×4+0.05×3×4+0.05×0.5×10+0.05×3×4+0.05×1×10+0.05×3×4+0.05×1.5×10=10.5,
∴当w=3时,估计该市居民该月的人均水费为10.5元
【解析】(1)由频率分布直方图得:用水量在[0.5,1)的频率为0.1,用水量在[1,1.5)的频率为0.15,用水量在[1.5,2)的频率为0.2,用水量在[2,2.5)的频率为0.25,用水量在[2.5,3)的频率为0.15,用水量在[3,3.5)的频率为0.05,用水量在[3.5,4)的频率为0.05,用水量在[4,4.5)的频率为0.05,由此能求出为使80%以上居民在该用的用水价为4元/立方米,w至少定为3立方米.(2)当w=3时,利用频率分布直方图能求出该市居民的人均水费.
【考点精析】通过灵活运用频率分布直方图,掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息即可以解答此题.