题目内容
已知数列{an}的各项均为正数,前n项的和Sn=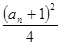
⑴ 求{an}的通项公式;
⑵ 设等比数列{bn}的首项为b,公比为2,前n项的和为Tn.若对任意n∈N*,Sn≤Tn
均成立,求实数b的取值范围.
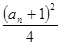
⑴ 求{an}的通项公式;
⑵ 设等比数列{bn}的首项为b,公比为2,前n项的和为Tn.若对任意n∈N*,Sn≤Tn
均成立,求实数b的取值范围.
(1) an=2n-1(n∈N*).(2) b≥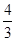 .
.
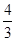 .
.试题分析: (1) a1=
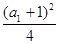 ,解得a1=1.
,解得a1=1.当n≥2时,由an=Sn-Sn-1=
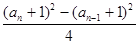 , -2
, -2得(an-an-1-2)(an+an-1)=0.
又因为an>0,所以an-an-1=2.
因此{an}是首项为1,公差为2的等差数列,
即an=2n-1(n∈N*). 6
(2) 因为Sn=n2,Tn=b(2n-1),
所以Sn≤Tn对任意n∈N*恒成立,
当且仅当
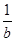 ≤
≤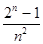 对任意n∈N*均成立.
对任意n∈N*均成立.令Cn=
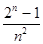 ,因为Cn+1-Cn=
,因为Cn+1-Cn=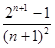 -
-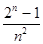 =
=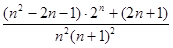 ,
,所以C1>C2,且当n≥2时,Cn<Cn+1.
因此
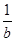 ≤C2=
≤C2=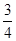 ,即b≥
,即b≥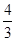 .
.点评:中档题,涉及数列的不等式证明问题,往往需要先求和、再证明。本题(2)通过研究数列的“单调性”,利用“放缩法”,达到证明目的。

练习册系列答案
相关题目
 的各项均为正数,其前
的各项均为正数,其前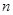 项和为
项和为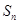 .若
.若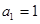 ,
,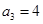 ,
,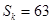 ,则
,则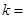 ___.
___.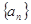 中,
中,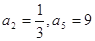 ,则
,则 。
。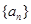 中
中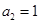 ,则其前3项的和
,则其前3项的和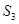 的取值范围是 ( )
的取值范围是 ( )
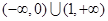


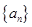 中,首项
中,首项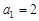 ,前3项和为14,则
,前3项和为14,则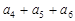 值为_____________.
值为_____________.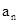 }中,如果
}中,如果 。
。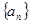 的公比为q,前n项和为
的公比为q,前n项和为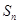 ,若
,若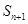 ,
,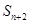 成等差数列,则公比q为( )
成等差数列,则公比q为( )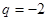
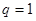

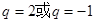
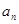 }的前
}的前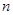 项和为
项和为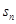 若
若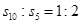 ,则
,则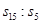 = ( )
= ( )