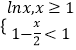题目内容
【题目】已知直线 
是椭圆 
的右准线，若椭圆的离心率为 
，右准线方程为x=2．
（1）求椭圆Γ的方程；
（2）已知一直线AB过右焦点F（c，0），交椭圆Γ于A，B两点，P为椭圆Γ的左顶点，PA，PB与右准线交于点M（xM ， yM），N（xN ， yN），问yMyN是否为定值，若是，求出该定值，否则说明理由．
【答案】
（1）解：依题意：椭圆的离心率e= 
= 
， 
=2，则a= 
，b=1，c=1，
故椭圆Γ方程为 
（2）解：设AB的方程：x=my+1，A（x1，y1），B（x2，y2），
则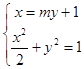 
，整理得：（m2+2）y2+2my﹣1=0，
△=（﹣2m）2+4（m2+2）＞0，
由韦达定理得：y1+y2=﹣ 
，y1y2=﹣ 
，
直线PA：y= 
（x+ ），
令x=2，得yM= 
（2+ ），
同理：yN= 
（2+ ），
∴yMyN= 
= 
，
= 
，
= 
，
= 
，
= 
= 
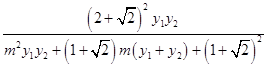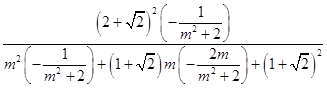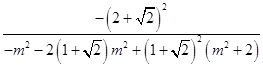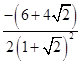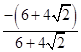=﹣1，
yMyN=﹣1，
yMyN是否为定值，定值为﹣1
【解析】（1）由题意可知：e= = ， =2，即可求得a和b的值，求得椭圆Γ的方程；（2）设AB的方程：x=my+1，代入椭圆方程由韦达定理求得直线PA的方程，代入即可求得yM= （2+ ），yN= （2+ ），yMyN= = ，代入即可求得yMyN=﹣1．
【题目】近年来共享单车在我国主要城市发展迅速．目前市场上有多种类型的共享单车，有关部门对其中三种共享单车方式（M方式、Y方式、F方式）进行统计（统计对象年龄在15～55岁），相关数据如表1，表2所示． 三种共享单车方式人群年龄比例（表1）
方式 | M | Y | F |
[15，25） | 25% | 20% | 35% |
[25，35） | 50% | 55% | 25% |
[35，45） | 20% | 20% | 20% |
[45，55] | 5% | a% | 20% |
不同性别选择共享单车种类情况统计（表2）
性别 | 男 | 女 |
1 | 20% | 50% |
2 | 35% | 40% |
3 | 45% | 10% |
（Ⅰ）根据表1估算出使用Y共享单车方式人群的平均年龄；
（Ⅱ）若从统计对象中随机选取男女各一人，试估计男性使用共享单车种类数大于女性使用共享单车种类数的概率；
（Ⅲ）现有一个年龄在25～35岁之间的共享单车用户，那么他使用Y方式出行的概率最大，使用F方式出行的概率最小，试问此结论是否正确？（只需写出结论）
