题目内容
【题目】如图,设椭圆C1: ![]() +
+ ![]() =1(a>b>0),长轴的右端点与抛物线C2:y2=8x的焦点F重合,且椭圆C1的离心率是
=1(a>b>0),长轴的右端点与抛物线C2:y2=8x的焦点F重合,且椭圆C1的离心率是 ![]() .
. 
(1)求椭圆C1的标准方程;
(2)过F作直线l交抛物线C2于A,B两点,过F且与直线l垂直的直线交椭圆C1于另一点C,求△ABC面积的最小值,以及取到最小值时直线l的方程.
【答案】
(1)解:∵椭圆C1: ![]() +
+ ![]() =1(a>b>0),长轴的右端点与抛物线C2:y2=8x的焦点F重合,∴a=2,
=1(a>b>0),长轴的右端点与抛物线C2:y2=8x的焦点F重合,∴a=2,
又∵椭圆C1的离心率是 ![]() .∴c=
.∴c= ![]() ,b=1,∴椭圆C1的标准方程:
,b=1,∴椭圆C1的标准方程: ![]()
(2)解:过点F(2,0)的直线l的方程设为:x=my+2,设A(x1,y1),B(x2,y2)
联立 ![]() 得y2﹣8my﹣16=0.
得y2﹣8my﹣16=0.
y1+y2=8m,y1y2=﹣16,∴|AB|= ![]() =8(1+m2).
=8(1+m2).
过F且与直线l垂直的直线设为:y=﹣m(x﹣2)
联立 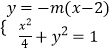 得(1+4m2)x2﹣16m2x+16m2﹣4=0,
得(1+4m2)x2﹣16m2x+16m2﹣4=0,
xC+2= ![]() ,xC=
,xC= ![]() .
.
∴|CF|= ![]()
![]() .
.
△ABC面积s= ![]() |AB||CF|=
|AB||CF|= ![]() .
.
令 ![]() ,则s=f(t)=
,则s=f(t)= ![]() ,f′(t)=
,f′(t)= ![]() ,
,
令f′(t)=0,则t2= ![]() ,即1+m2=
,即1+m2= ![]() 时,△ABC面积最小.
时,△ABC面积最小.
即当m=± ![]() 时,△ABC面积的最小值为9,此时直线l的方程为:x=±
时,△ABC面积的最小值为9,此时直线l的方程为:x=± ![]() y+2
y+2
【解析】(1)由已知可得a,又由椭圆C1的离心率得c,b=1即可.(2)过点F(2,0)的直线l的方程设为:x=my+2,设A(x1 , y1),B(x2 , y2)联立 ![]() 得y2
得y2![]() ,同理得|CF|=
,同理得|CF|= ![]()
![]() .△ABC面积s=
.△ABC面积s= ![]() |AB||CF|=
|AB||CF|= ![]() .令
.令 ![]() ,则s=f(t)=
,则s=f(t)= ![]() ,利用导数求最值即可.
,利用导数求最值即可.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目