题目内容
已知函数f(x)的定义域为N*,且f(x+1)=f(x)+x,f(1)=0.(1)求f(x)的解析式.
(2)设
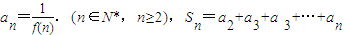 ,问是否存在最大的正整数m,使得对任意的n∈N*均有
,问是否存在最大的正整数m,使得对任意的n∈N*均有 恒成立?若存在,求出m值;若不存在请说明理由.
恒成立?若存在,求出m值;若不存在请说明理由.
【答案】分析:(1)令x=n,可得f(n+1)-f(n)=n,利用叠加法,可求函数f(x)的解析式;
(2)先裂项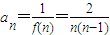 =2(
=2(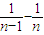 )(n≥2),再求和,确定Sn(n≥2)递增,可得(Sn)min=a2=1,对任意的n∈N*均有
)(n≥2),再求和,确定Sn(n≥2)递增,可得(Sn)min=a2=1,对任意的n∈N*均有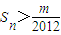 恒成立,转化为
恒成立,转化为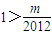 ,由此可得结论.
,由此可得结论.
解答:解:(1)令x=n,则由f(x+1)=f(x)+x可得f(n+1)-f(n)=n
∴f(n)=f(1)+[f(2)-f(1)]+…+[f(n)-f(n-1)]=1+2+…+(n-1)= (n≥2)
(n≥2)
n=1时,f(1)=0也满足上式
∴
∴f(x)=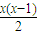 ;
;
(2)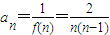 =2(
=2(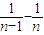 )(n≥2)
)(n≥2)
∴Sn=2[(1- )+(
)+(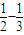 )+…+(
)+…+(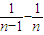 )]=2-
)]=2-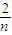
∵n≥2时,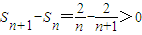
∴Sn(n≥2)递增,
∴(Sn)min=a2=1
∵对任意的n∈N*均有 恒成立
恒成立
∴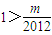
∴m<2012
∴最大的正整数m为2011.
点评:本题考查函数的解析式,考查数列与函数的关系,考查叠加法,考查裂项法求数列的和,考查恒成立问题,综合性强.
(2)先裂项
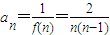 =2(
=2(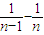 )(n≥2),再求和,确定Sn(n≥2)递增,可得(Sn)min=a2=1,对任意的n∈N*均有
)(n≥2),再求和,确定Sn(n≥2)递增,可得(Sn)min=a2=1,对任意的n∈N*均有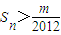 恒成立,转化为
恒成立,转化为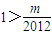 ,由此可得结论.
,由此可得结论.解答:解:(1)令x=n,则由f(x+1)=f(x)+x可得f(n+1)-f(n)=n
∴f(n)=f(1)+[f(2)-f(1)]+…+[f(n)-f(n-1)]=1+2+…+(n-1)=
 (n≥2)
(n≥2)n=1时,f(1)=0也满足上式
∴

∴f(x)=
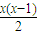 ;
;(2)
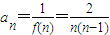 =2(
=2(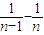 )(n≥2)
)(n≥2)∴Sn=2[(1-
 )+(
)+(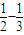 )+…+(
)+…+(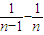 )]=2-
)]=2-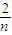
∵n≥2时,
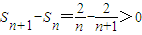
∴Sn(n≥2)递增,
∴(Sn)min=a2=1
∵对任意的n∈N*均有
 恒成立
恒成立∴
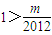
∴m<2012
∴最大的正整数m为2011.
点评:本题考查函数的解析式,考查数列与函数的关系,考查叠加法,考查裂项法求数列的和,考查恒成立问题,综合性强.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
