题目内容
12.已知函数f(x)=$\frac{x}{{x}^{2}+1}$,构造数列an=f(n)(n∈N+),写出数列{an}的前5项,并判断该数列的单调性.分析 由题意可得:an=$\frac{n}{{n}^{2}+1}$,分别令n=1,2,3,4,5即可得出.由以上可猜想数列{an}单调递减.再利用导数研究函数f(x)=$\frac{x}{{x}^{2}+1}$(x≥1)的单调性即可得出.
解答 解:由题意可得:an=$\frac{n}{{n}^{2}+1}$,
∴a1=$\frac{1}{2}$,a2=$\frac{2}{5}$,a3=$\frac{3}{10}$,a4=$\frac{4}{17}$,a5=$\frac{5}{26}$.
由以上可猜想数列{an}单调递减.
下面给出证明:f′(x)=$\frac{{x}^{2}+1-x×2x}{({x}^{2}+1)^{2}}$=$\frac{-(x+1)(x-1)}{({x}^{2}+1)^{2}}$,
当x≥1时,f′(x)≤0,因此函数f(x)在x≥1时单调递增.
∴数列{an}单调递增.
点评 本题考查了利用导数研究函数的单调性、数列的单调性、通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
17.已知f(x)=(x-1)2+1,则f(x+1)等于( )
| A. | (x+2)2+1 | B. | x2+1 | C. | (x-2)2+1 | D. | 4x2+1 |
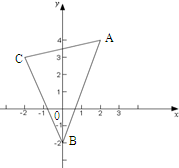 如图,已知△ABC的顶点为A(2,4),B(0,-2),C(-2,3),求:
如图,已知△ABC的顶点为A(2,4),B(0,-2),C(-2,3),求: