题目内容
已知二次函数 满足
满足 且
且 .
.
(Ⅰ)求 的解析式.(Ⅱ)在区间
的解析式.(Ⅱ)在区间 上,
上,  的图象恒在
的图象恒在 的图象上方 试确定实数
的图象上方 试确定实数 的范围.
的范围.
 满足
满足 且
且 .
.(Ⅰ)求
 的解析式.(Ⅱ)在区间
的解析式.(Ⅱ)在区间 上,
上,  的图象恒在
的图象恒在 的图象上方 试确定实数
的图象上方 试确定实数 的范围.
的范围. (Ⅰ)f(x)=x2-x+1. (Ⅱ)m<-1.
本试题主要是考查了函数的性质和函数的解析式的运用
(1)设f(x)=ax2+bx+c,由f(0)=1得c=1,故f(x)=ax2+bx+1.
∵f(x+1)-f(x)=2x,∴a(x+1)2+b(x+1)+1-(ax2+bx+1)=2x.
即2ax+a+b=2x,
(2)由题意得x2-x+1>2x+m在[-1,1]上恒成立.即x2-3x+1-m>0在[-1, 1]上恒成立.
设g(x)= x2-3x+1-m,其图象的对称轴为直线x= ,所以g(x) 在[-1,1]上递减.
,所以g(x) 在[-1,1]上递减.
那么可得。
解: (Ⅰ)设f(x)=ax2+bx+c,由f(0)=1得c=1,故f(x)=ax2+bx+1.
∵f(x+1)-f(x)=2x,∴a(x+1)2+b(x+1)+1-(ax2+bx+1)=2x.
即2ax+a+b=2x,所以 ,∴f(x)=x2-x+1.
,∴f(x)=x2-x+1. 
(Ⅱ)由题意得x2-x+1>2x+m在[-1,1]上恒成立.即x2-3x+1-m>0在[-1, 1]上恒成立.
设g(x)= x2-3x+1-m,其图象的对称轴为直线x= ,所以g(x) 在[-1,1]上递减.
,所以g(x) 在[-1,1]上递减.
故只需g(1)>0,即12-3×1+1-m>0,解得m<-1.
(1)设f(x)=ax2+bx+c,由f(0)=1得c=1,故f(x)=ax2+bx+1.
∵f(x+1)-f(x)=2x,∴a(x+1)2+b(x+1)+1-(ax2+bx+1)=2x.
即2ax+a+b=2x,
(2)由题意得x2-x+1>2x+m在[-1,1]上恒成立.即x2-3x+1-m>0在[-1, 1]上恒成立.
设g(x)= x2-3x+1-m,其图象的对称轴为直线x=
 ,所以g(x) 在[-1,1]上递减.
,所以g(x) 在[-1,1]上递减.那么可得。
解: (Ⅰ)设f(x)=ax2+bx+c,由f(0)=1得c=1,故f(x)=ax2+bx+1.
∵f(x+1)-f(x)=2x,∴a(x+1)2+b(x+1)+1-(ax2+bx+1)=2x.
即2ax+a+b=2x,所以
 ,∴f(x)=x2-x+1.
,∴f(x)=x2-x+1. 
(Ⅱ)由题意得x2-x+1>2x+m在[-1,1]上恒成立.即x2-3x+1-m>0在[-1, 1]上恒成立.
设g(x)= x2-3x+1-m,其图象的对称轴为直线x=
 ,所以g(x) 在[-1,1]上递减.
,所以g(x) 在[-1,1]上递减.故只需g(1)>0,即12-3×1+1-m>0,解得m<-1.

练习册系列答案
相关题目
 ,方程
,方程 的两根
的两根 和
和 满足
满足 .
. 的取值范围;
的取值范围; 与
与 的大小.并说明理由.
的大小.并说明理由. 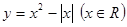 的图像,并指出它的单调区间.
的图像,并指出它的单调区间.
 对任意实数t都有f (3+ t) =" f" (3-t),那么( )
对任意实数t都有f (3+ t) =" f" (3-t),那么( )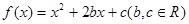 满足
满足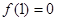 ,且关于
,且关于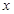 的方程
的方程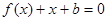 的两实数根分别在区间(-3,-2),(0,1)内。
的两实数根分别在区间(-3,-2),(0,1)内。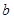 的取值范围;
的取值范围;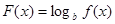 在区间(-1-
在区间(-1-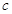 ,1-
,1-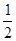 ,1]是单调函数,则a的取值范围是 ( )
,1]是单调函数,则a的取值范围是 ( ) 的单调递增区间是
的单调递增区间是 ,则
,则 = .
= .
 ,若
,若 ,(其中
,(其中 ),则实数
),则实数 的取值范围是 .
的取值范围是 .