题目内容

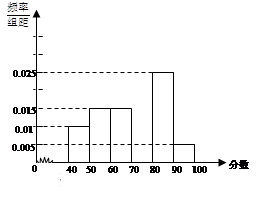
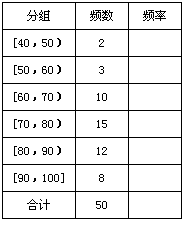
某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本，得频率分布表如下：

组号
分组
频数
频率
第一组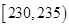

8
0.16
第二组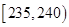

①
0.24
第三组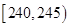

15
②
第四组

10
0.20
第五组

5
0.10
合             计
50
1.00
(1)写出表中①②位置的数据；
(2)为了选拔出更优秀的学生，高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核，分别求第三、四、五各组参加考核人数；
(3)在(2)的前提下，高校决定在这6名学生中录取2名学生，求2人中至少有1名是第四组的概率．

(1) 12、0.3 (2)3,2,1 (3)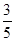

解析试题分析：(1) ①②位置的数据分别为50-8-15-10-5=12、1-0.16-1.24-0.20-0.10=0.3；   4分
(2) 第三、四、五组总人数之比为15:10:5，所以抽取的人数之比为3:2:1，即抽取参加考核人数分别为3、2、1； 8分
(3) 设上述6人为abcdef(其中第四组的两人分别为d，e)，则从6人中任取2人的所有情形为：{ab，ac，ad，ae，af，bc，bd，be，bf，cd，ce，cf，de，df，ef}
共有15种．10分
记“2人中至少有一名是第四组”为事件A，则事件A所含的基本事件的种数有9种． 12分
所以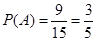，故2人中至少有一名是第四组的概率为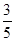． 14分
考点：频率分布表，分层抽样即古典概型概率
点评：频率分布表中各组频数之和为合计总数，频率之和为1；分层抽样是按各层元素的个数比例抽取样本；古典概型概率主要是找到所有基本事件种数与满足题意要求的基本事件种数，然后求其比值

练习册系列答案
相关题目

给出施化肥量（kg）对水稻产量（kg）影响的试验数据：

施化肥量x
 		15
 		20
 		25
 		30
 
水稻产量y
 		330
 		345
 		365
 		405
 
（1）试求出回归直线方程；
（2）请估计当施化肥量为10时，水稻产量为多少？
（已知：7.5×31.25+2.5×16.25+2.5×3.75+7.5×43.75=612.5,2×7.5×7.5+2×2.5×2.5=125）

我校高三年级进行了一次水平测试.用系统抽样的方法抽取了50名学生的数学成绩,准备进行分析和研究.经统计成绩的分组及各组的频数如下:
[40,50), 2;   [50,60), 3;  [60,70), 10;  [70,80), 15;   [80,90), 12;  [90,100], 8.
（Ⅰ）完成样本的频率分布表；画出频率分布直方图.
（Ⅱ）估计成绩在85分以下的学生比例；
（Ⅲ）请你根据以上信息去估计样本的众数、中位数、平均数.（精确到0.01）
频率分布表                       频率分布直方图
     

某重点中学的高二英语老师Vivien，为调查学生的单词记忆时间开展问卷调查。发现在回收上来的1000份有效问卷中，有600名同学们背英语单词的时间安排在白天，另外400名学生晚上临睡前背。Vivien老师用分层抽样的方法抽取50名学生进行实验，实验方法是使两组学生记忆40个无意义音节（如XIQ、GEH），均要求在刚能全部记清时就停止识记，并在8小时后进行记忆测验。不同的是，甲组同学识记结束后一直不睡觉，8小时后测验；乙组同学识记停止后立刻睡觉，8小时后叫醒测验。
乙组同学识记停止8小时后的准确回忆（保持）情况如图。

（1）由分层抽样方法，抽取的50名学生乙组应有几名？
（2）从乙组准确回忆音节数在[8,20)范围内的学生中随机选2人，求两人均准确回忆12个（含12个）以上的概率；
（3）若从是否睡前记忆单词和单词小测能否优秀进行统计，运用22列联表进行独立性检验，经计算K2=4．069，参考下表你能得到什么统计学结论？

P(K≥k0)
 		0.100
 		0.050
 		0.025
 		0.010
 		0.001
 

某种产品的广告费用支出(百万)与销售额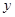(百万)之间有如下的对应数据:


2
4
5
6
8

30
40
60
50
70
(1)画出散点图;
(2)求回归直线方程;
(3)据此估计广告费用为10(百万)时,销售收入的值.

某单位为了提高员工素质，举办了一场跳绳比赛，其中男员工12人，女员工18人，其成绩编成如图所示的茎叶图（单位：分），分数在175分以上（含175分）者定为“运动健将”，并给予特别奖励，其他人员则给予“运动积极分子”称号.

（1）若用分层抽样的方法从“运动健将”和“运动积极分子”中抽取10人，然后再从这10人中选4人，求至少有1人是“运动健将”的概率；
（2）若从所有“运动健将”中选3名代表，求所选代表中女“运动健将”恰有2人的概率.

为了调查胃病是否与生活规律有关，调查某地540名40岁以上的人得结果如下：

 
患胃病
未患胃病
合计
生活不规律
60
260
320
生活有规律
20
200
220
合计
80
460
540
根据以上数据回答40岁以上的人患胃病与生活规律有关吗？

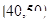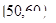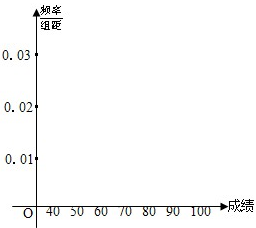
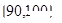某校从高一年级学生中随机抽取40名学生作为样本，将他们的期中考试数学成绩（满分100分，成绩均为不低于40分的整数）分成六组：，，…，后得到如图的频率分布直方图．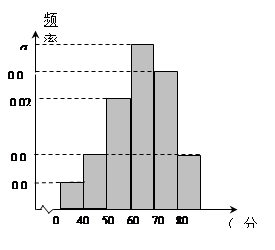

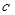（Ⅰ）求图中实数的值；
（Ⅱ）若该校高一年级共有学生500人，试估计该校高一年级在这次考试中成绩不低于60分的人数；
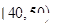(Ⅲ)若从样本中数学成绩在与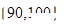两个分数段内的学生中随机选取两名学生,试用列举
法求这两名学生的数学成绩之差的绝对值不大于10的概率.

（本小题满分12分）
某校从参加考试的学生中抽出60名学生，将其成绩（均为整数）分成六组[40，50），[50，60）．．．[90，100]后画出如下部分频率分布直方图.观察图形的信息，回答下列问题：

（1）求成绩落在[70，80）上的频率，并补全这个频率分布直方图；
（2）估计这次考试的及格率（60分及以上为及格）；
（3）把90分以上（包括90分）视为成绩优秀，那么从成绩是60分以上（包括60分）的学生中选一人，求此人成绩优秀的概率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网