题目内容
【题目】三棱锥
中，
，△
为等边三角形，二面角
的余弦值为
，当三棱锥的体积最大时，其外接球的表面积为
.则三棱锥体积的最大值为（ ）
A.
B.
C.
D.
【答案】D
【解析】
由已知作出图象，找出二面角
的平面角，设出
的长，即可求出三棱锥
的高，然后利用基本不等式即可确定三棱锥体积的最大值（用含有
长度的字母表示），再设出球心
，由球的表面积求得半径，根据球的几何性质，利用球心距，半径，底面半径之间的关系求得的长度，则三棱锥体积的最大值可求.
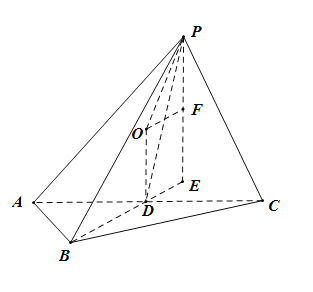
如图所示，过点
作
面
，垂足为
，过点作
交于点
，连接
，
则
为二面角
的平面角的补角，即有
，
易知
面
，则
，而△
为等边三角形，
∴为中点，
设
，
则
c
，
故三棱锥的体积为：
，
当且仅当
时，体积最大，此时
共线.
设三棱锥的外接球的球心为，半径为
，
由已知，
，得
.
过点作
于F，则四边形
为矩形，
则
， 
，
，
在
△
中
，解得
∴三棱锥的体积的最大值为：
.
故选：D.
【题目】
指数是用体重公斤数除以身高米数的平方得出的数字，是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准．对于高中男体育特长生而言，当数值大于或等于20.5时，我们说体重较重，当数值小于20.5时，我们说体重较轻，身高大于或等于
我们说身高较高，身高小于170cm我们说身高较矮．
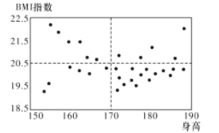
（Ⅰ）已知某高中共有32名男体育特长生，其身高与
指数的数据如散点图，请根据所得信息，完成下述列联表，并判断是否有
的把握认为男生的身高对指数有影响．
身高较矮 | 身高较高 | 合计 | |
体重较轻 | |||
体重较重 | |||
合计 |
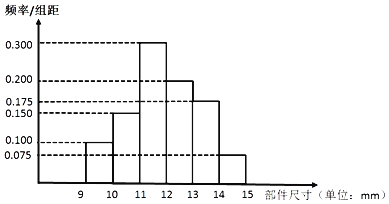
（Ⅱ）①从上述32名男体育特长生中随机选取8名，其身高和体重的数据如表所示：
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
身高 | 166 | 167 | 160 | 173 | 178 | 169 | 158 | 173 |
体重 | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
根据最小二乘法的思想与公式求得线性回归方程为
．利用已经求得的线性回归方程，请完善下列残差表，并求
（解释变量（身高）对于预报变量（体重）变化的贡献值）（保留两位有效数字）；
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
体重（kg） | 58 | 53 | 61 | 66 | 57 | 50 | 66 | |
残差 |
|
|
|
|
|
|
|
②通过残差分析，对于残差的最大（绝对值）的那组数据，需要确认在样本点的采集中是否有人为的错误，已知通过重新采集发现，该组数据的体重应该为
．小明重新根据最小二乘法的思想与公式，已算出
，请在小明所算的基础上求出男体育特长生的身高与体重的线性回归方程．
参考数据：
，
，
，
，
参考公式：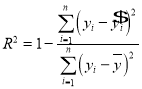
，
，
，
，
．
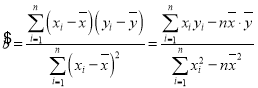| 0.10 | 0.05 | 0.01 | 0.005 |
| 2.706 | 3.811 | 6.635 | 7.879 |
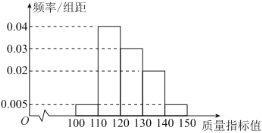
【题目】按照水果市场的需要等因素，水果种植户把某种成熟后的水果按其直径
的大小分为不同等级.某商家计划从该种植户那里购进一批这种水果销售.为了了解这种水果的质量等级情况，现随机抽取了100个这种水果，统计得到如下直径分布表（单位：mm）：
d |
|
|
|
|
|
等级 | 三级品 | 二级品 | 一级品 | 特级品 | 特级品 |
频数 | 1 | m | 29 | n | 7 |
用分层抽样的方法从其中的一级品和特级品共抽取6个，其中一级品2个.
（1）估计这批水果中特级品的比例；
（2）已知样本中这批水果不按等级混装的话20个约1斤，该种植户有20000斤这种水果待售，商家提出两种收购方案：
方案A：以6.5元/斤收购；
方案B：以级别分装收购，每袋20个，特级品8元/袋，一级品5元/袋，二级品4元/袋，三级品3元/袋.
用样本的频率分布估计总体分布，问哪个方案种植户的收益更高？并说明理由.
