题目内容
阅读:
已知 、
、 ,
, ,求
,求 的最小值.
的最小值.
解法如下: ,
,
当且仅当 ,即
,即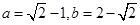 时取到等号,
时取到等号,
则 的最小值为
的最小值为 .
.
应用上述解法,求解下列问题:
(1)已知 ,
, ,求
,求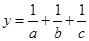 的最小值;
的最小值;
(2)已知 ,求函数
,求函数 的最小值;
的最小值;
(3)已知正数 、
、 、
、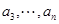 ,
, ,
,
求证: .
.
(1)9;(2)18;(3)证明见解析.
解析试题分析:本题关键是阅读给定的材料,弄懂弄清给定材料提供的方法(“1”的代换),并加以运用.主要就是 ,展开后就可应用基本不等式求得最值.(1)
,展开后就可应用基本不等式求得最值.(1)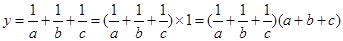 ;(2)虽然没有已知的“1”,但观察求值式子的分母,可以凑配出“1”:
;(2)虽然没有已知的“1”,但观察求值式子的分母,可以凑配出“1”: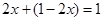 ,因此有
,因此有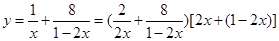 ,展开后即可应用基本不等式;(3)观察求证式的分母,结合已知有
,展开后即可应用基本不等式;(3)观察求证式的分母,结合已知有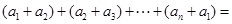
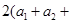
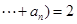 ,因此有
,因此有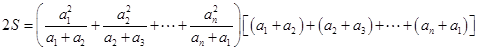
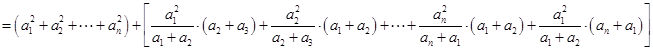 此式中关键是凑配出基本不等式所需要的两项,如
此式中关键是凑配出基本不等式所需要的两项,如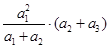 与
与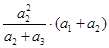 合并相加利用基本不等式有
合并相加利用基本不等式有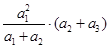
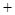
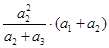
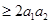 ,从而最终得出
,从而最终得出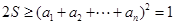 .
.
(1)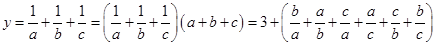 ,
,
2分
而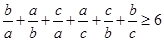 ,
,
当且仅当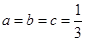 时取到等号,则
时取到等号,则 ,即
,即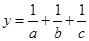 的最小值为
的最小值为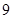 . 5分
. 5分
(2)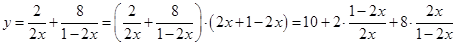 , 7分
, 7分
而 ,
,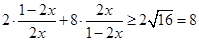 ,
,
当且仅当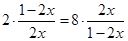 ,即
,即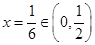 时取到等号,则
时取到等号,则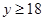 ,
,
所以函数 的最小值为
的最小值为 . 10分
. 10分
(3)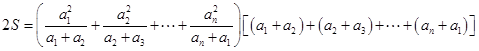
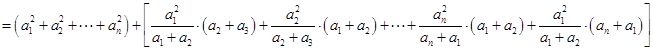
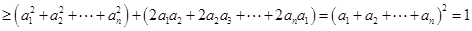
当且仅当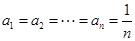 时取到等号,则
时取到等号,则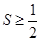 . 16分
. 16分
考点:阅读材料问题,“1”的代换,基本不等式.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 ,(x>0,
,(x>0,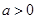 ).
).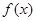 >-x+4,求实数
>-x+4,求实数 的取值范围
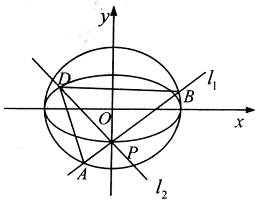
的取值范围 是椭圆
是椭圆 的一个顶点,
的一个顶点, 的长轴是圆
的长轴是圆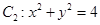 的直径,
的直径,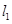 、
、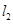 是过点
是过点 且互相垂直的两条直线,其中
且互相垂直的两条直线,其中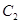 于
于 、
、 两点,
两点, .
.
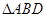 面积的最大值及取得最大值时直线
面积的最大值及取得最大值时直线 都是正数,
都是正数,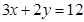 ,求
,求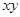 的最大值
的最大值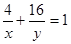 ,求
,求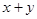 的最小值.
的最小值.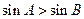 ;②若对一切
;②若对一切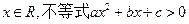 恒成立,则必有
恒成立,则必有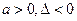 ;③不等式
;③不等式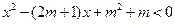 的解集为
的解集为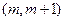 ;④函数
;④函数 最小值为2,其中正确的序号为__________ 。
最小值为2,其中正确的序号为__________ 。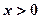 ,则
,则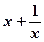 的最小值为 .
的最小值为 .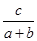 +
+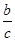 的最小值.
的最小值.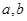 为正数,且
为正数,且 .求
.求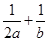 的最小值.
的最小值.